Si përcaktohet shenja e momentit? Statika. Momenti i fuqisë. Kursi bazë i leksioneve për forcën e materialeve, teorinë, praktikën, detyrat

Udhëzimet

Le të jetë Q pika për të cilën merret parasysh momenti i forcës. Kjo pikë quhet pol. Vizatoni një vektor të rrezes r nga kjo pikë deri në pikën e zbatimit të forcës F. Atëherë momenti i forcës M përcaktohet si prodhim vektorial i r nga F: M=.

Rezultati i një produkti kryq është një vektor. Gjatësia e vektorit shprehet me modulin: |M|=|r|·|F|·sinφ, ku φ është këndi ndërmjet r dhe F. Vektori M është ortogonal me vektorin r dhe me vektorin F: M⊥r , M⊥F.

Vektori M drejtohet në atë mënyrë që trefishi i vektorëve r, F, M është i drejtë. Si të përcaktohet se një trefish i vektorëve është i drejtë? Imagjinoni që ju (syri juaj) jeni në fund të vektorit të tretë dhe shikoni dy vektorët e tjerë. Nëse kalimi më i shkurtër nga vektori i parë tek i dyti duket se ndodh në drejtim të kundërt të akrepave të orës, ai është një vektor i trefishtë djathtas. Përndryshe, ke të bësh me një tre të majtë.

Pra, kombinoni origjinën e vektorëve r dhe F. Kjo mund të bëhet me transferim paralel të vektorit F në pikën Q. Tani, përmes së njëjtës pikë, vizatoni një bosht pingul me rrafshin e vektorëve r dhe F. Ky bosht do të jetë pingul me vektorët menjëherë. Këtu, në parim, ekzistojnë vetëm dy mundësi për drejtimin e momentit të forcës: lart ose poshtë.

Mundohuni të drejtoni momentin e forcës F lart, vizatoni një shigjetë vektoriale në bosht. Nga kjo shigjetë, shikoni vektorët r dhe F (mund të përdorni një sy simbolik). Kalimi më i shkurtër nga r në F mund të tregohet me një shigjetë të rrumbullakosur. A është e drejtë trefishi i vektorëve r, F, M? A është shigjeta në drejtim të kundërt të akrepave të orës? Nëse po, atëherë jeni në drejtimin e duhur për momentin e forcës F. Nëse jo, atëherë duhet të ndryshoni drejtimin në të kundërt.

Ju gjithashtu mund të përcaktoni drejtimin e momentit të forcës duke përdorur rregullin e dorës së djathtë. Drejtoni gishtin tuaj tregues me vektorin e rrezes. Lidhni gishtin tuaj të mesëm me vektorin e forcës. Nga fundi i gishtit të madh, shikoni dy vektorët. Nëse kalimi nga treguesi në gishtin e mesëm kryhet në drejtim të kundërt të akrepave të orës, atëherë drejtimi i momentit të forcës përkon me drejtimin që tregon gishti i madh. Nëse kalimi ndodh në drejtim të akrepave të orës, atëherë drejtimi i momentit të forcës është i kundërt me të.

Rregulli i gimletit është shumë i ngjashëm me rregullin e dorës. Me katër gishtat e dorës tuaj të djathtë, rrotulloni një vidë nga r në F. Produkti vektor do të ketë drejtimin në të cilin është përdredhur gjilpëra gjatë një rrotullimi të tillë mendor.

Le të vendoset tani pika Q në të njëjtën vijë që përmban vektorin e forcës F. Atëherë vektori i rrezes dhe vektori i forcës do të jenë kolinear. Në këtë rast, produkti i tyre vektor degjeneron në një vektor zero dhe përfaqësohet nga një pikë. Vektori null nuk ka drejtim specifik, por konsiderohet i bashkëdrejtuar me çdo vektor tjetër.

Për të llogaritur saktë efektin e një force që rrotullon një trup, përcaktoni pikën e zbatimit të saj dhe distancën nga kjo pikë në boshtin e rrotullimit. Kjo është e rëndësishme për përcaktimin e karakteristikave teknike të mekanizmave të ndryshëm. Çift rrotullimi i një motori mund të llogaritet nëse dihet fuqia dhe shpejtësia e tij.

Do t'ju duhet

• Sundimtar, dinamometër, takometër, testues, Teslametër.

Udhëzimet

Përcaktoni pikën ose boshtin rreth të cilit trupi. Gjeni pikën ku ushtrohet forca. Lidhni pikën e aplikimit të forcës dhe pikën e rrotullimit, ose ulni pingulën me boshtin e rrotullimit. Matni këtë distancë, është "krahu i forcës". Merrni matje në metra. Matni forcën në njuton duke përdorur një dinamometër. Matni këndin midis krahut dhe vektorit të forcës. Për të llogaritur momentin rrotullues, gjeni prodhimin e forcës dhe sinusit të këndit ndërmjet tyre M=F r sin(α). Rezultati do të jetë në njuton për metër.

Mekanika teorike. Statika:

Sistemi i forcave konvergjente
Përkufizimi dhe Teorema e Tre Forcave
Përkufizimi grafik i rezultantes së forcave konvergjente
Detyrë analitike e forcës
Përcaktimi analitik i rezultantit të forcave konvergjente
Kushtet dhe ekuacionet e ekuilibrit për një sistem forcash konvergjente
Zgjidhja e problemeve
★ Ekuilibri nën veprimin e një sistemi forcash konvergjente

Teoria e çiftit të forcës

Çifti i forcave dhe vetitë e tij
Teorema e ekuivalencës së çifteve
Mbledhja e çifteve të forcave
Ekuilibri i sistemeve çift

Sjellja e një sistemi të rrafshët të forcave
Lema e Poinsot-it
Teorema mbi zvogëlimin e një sistemi të rrafshët të forcave
Raste të veçanta të reduktimit të një sistemi të rrafshët të forcave
Sistemi i ekuilibruar i forcave

Përcaktimi i reaksioneve mbështetëse të sistemeve me shufra të sheshta
★ Ekuilibri nën veprimin e një sistemi forcash paralele në një rrafsh
Sistemi i forcës paralele
Sistemi arbitrar i sheshtë i forcave
Sistemi arbitrar i sheshtë i forcave. RGR 1
★ Ekuilibri i një sistemi arbitrar forcash të rrafshët
Llogaritja e sistemeve të përbëra
Llogaritja e sistemeve të përbëra. RGR 2
★ Ekuilibri i një sistemi trupash 1
★ Ekuilibri i një sistemi trupash 2
★ Ekuilibri i sistemit të trupave 3
Përcaktimi grafik i reaksioneve mbështetëse

subjektet:termeh:statikë:momenti_force_relativ_në_qendrën

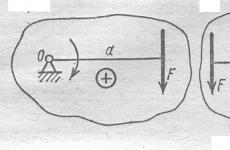
Le të shqyrtojmë një trup që është i fiksuar në qendër O dhe mund të rrotullohet rreth një boshti që kalon nga pika O dhe pingul me rrafshin e vizatimit. Le të zbatojmë forcën P në pikën A të këtij trupi dhe të zbulojmë se çfarë përcakton veprimin rrotullues të kësaj force ( Fig.1).

Është e qartë se efekti i një force në një trup do të varet jo vetëm nga madhësia e tij, por edhe nga mënyra se si ai drejtohet dhe në fund do të përcaktohet nga moment rreth qendrës O.

Përkufizimi 1. Momenti i forcës P në lidhje me qendrën O është prodhimi i modulit të forcës dhe shpatullës së tij të marrë me shenjën $\pm$ - domethënë gjatësia e pingulit të ulur nga pika e momentit në vijë. të veprimit të forcës.

Rregulli i shenjës: momenti i forcës konsiderohet pozitiv nëse forca tenton të rrotullojë trupin në drejtim të kundërt dhe negativ nëse e rrotullon trupin në drejtim të akrepave të orës.

Në përputhje me këtë përkufizim, momenti i forcës është numerikisht i barabartë me sipërfaqen e dyfishtë të trekëndëshit OAB, i ndërtuar në vektorin e forcës P me kulmin në pikën e momentit: $M_0(P) = P\cdot d = 2S \Delta_(OAB)$ .

Vini re se momenti i forcës në lidhje me pikën O është i barabartë me zero nëse vija e veprimit e forcës kalon nëpër pikën e momentit.

Përkufizimi i konsideruar i momentit të forcës është i përshtatshëm vetëm për një sistem të rrafshët të forcave. Në rastin e përgjithshëm, për të përshkruar pa mëdyshje veprimin rrotullues të një force, ne prezantojmë përkufizimin e mëposhtëm.

Përkufizimi 2. Vektori-momenti i forcës P në lidhje me qendrën O është një vektor që:

zbatohet në pikën e momentit O pingul me rrafshin e një trekëndëshi të ndërtuar mbi vektorin e forcës me kulmin në pikën momentale;

drejtuar sipas rregullit të vidës së djathtë;

e barabartë në madhësi me momentin e forcës P në lidhje me qendrën O (Fig.1a).

Rregulli i vidës së djathtë, i njohur edhe nga kurset e fizikës si rregull gimlet, do të thotë se nëse shikojmë drejt momentit-vektor $\vec(M_0)(\vec(P))$ , do të shohim rrotullimin e planit të veprimit të tij nga forca $\vec(P)$, që ndodh në drejtim të kundërt të akrepave të orës. .

Le të shënojmë me $\vec(r)$ vektorin e rrezes së pikës së aplikimit të forcës $\vec(P)$ dhe të vërtetojmë se sa vijon është e vërtetë

Teorema 1. Vektori-momenti i forcës $\vec(P)$ në raport me qendrën RRETHështë e barabartë me produktin vektorial të vektorit të rrezes $\vec(r)$ dhe vektorit të forcës $\vec(P)$:

$$\vec(M_0)(\vec(P)) = (\vec(r) \herë \vec(P))$$

Kujtojmë se prodhimi vektorial i vektorëve $\vec(a)\text( dhe )\vec(b)$ është vektori $\vec(c)$, i cili ( Fig.2b):

është pingul me vektorët $\vec(a)\text( dhe )\vec(b)$ ;

formon me to një treshe vektorësh në krahun e djathtë, domethënë drejtohet në atë mënyrë që, duke parë drejt këtij vektori, do të shohim një rrotullim nga vektori $\vec(a)$ në vektorin $\vec( b)$ në këndin më të vogël, që ndodh në drejtim të kundërt të akrepave të orës;

e barabartë në madhësi me dyfishin e sipërfaqes së trekëndëshit të ndërtuar mbi këta vektorë:

$$|\vec(c)| = |\vec(a) \herë \vec(b)| = |\vec(a)|\cdot|\vec(b)|\cdot\sin(\vec(a),\,\vec(b))$$

Për të vërtetuar teoremën, vëmë re, së pari, se një vektor i barabartë me produktin vektorial të vektorëve $\vec(r)\text( dhe )\vec(P)$ do të jetë kolinear me vektorin $\vec(M_0) (\vec(P))$ .

Për ta verifikuar këtë, mjafton të vizatohen këta vektorë nga një pikë ( Fig.1c). Pra, $(\vec(r) \times \vec(P)) \uparrow \uparrow \vec(M_0)(\vec(P))$.

Së dyti, moduli i produktit vektorial të këtyre vektorëve do të jetë i barabartë me:

$$|\vec(r) \times \vec(P)| = |\vec(r)|\cdot|\vec(P)|\cdot\sin(\vec(r),\,\vec(P)) = P \cdot d =|\vec(M_0)(\ vec(P))|$$

Këtu vijon lidhja e teoremës.

Pasoja e kësaj teoreme është:

Teorema e Varignon-it (për momentin e rezultantes së forcave konvergjente). Momenti vektor i sistemit rezultant të forcave konvergjente në lidhje me një qendër arbitrare O është e barabartë me shumën gjeometrike të momenteve vektoriale të të gjitha forcave të sistemit në lidhje me këtë qendër:

$$\vec(M_0)(\vec(R)) = \sum_(i=1)^(i=n)\vec(M_(0\,\,i))(\vec(P_i))$$

Në fakt, momenti i rezultantit, duke marrë parasysh Teorema 1 dhe përkufizimi analitik i rezultatit të forcave konvergjente do të jetë i barabartë me:

$$ \vec(M_0)(\vec(R))= \vec(R)\herë\vec(r) \,\,\,\;\;\tekst( , sepse ) \vec(M_0 )(\ vec(P)) = (\vec(r) \herë \vec(P)) \\ \vec(R)\herë\vec(r)= \vec(r)\herë\sum_(i= 1)^ (i=n)\vec(P_i) \,\,\,\;\;\tekst( , sepse ) (\vec(P_1), \vec(P_2), \dots, \vec (P_n)) \sim \vec(R) = \sum_(i=1)^(i=n) \vec(P_i) \\ \vec(r)\herë\sum_(i=1)^(i= n)\vec(P_i ) = \sum_(i=1)^(i=n)(\vec(r)\herë\vec(P_i)) = \sum_(i=1)^(i=n)\ vec(M_(0\ ,\,i))(\vec(P_i)) $$

Për një sistem të rrafshët të forcave konvergjente, shuma gjeometrike në Teorema e Varignon-it shkon në algjebrike:

$$M_0(R)=\sum_(i=1)^(i=n)M_(0\,\,i)(\vec(P_i))$$

shënim

Në literaturën arsimore, termi "moment" përdoret për të treguar si momentin e një force ashtu edhe momentin e saj vektor.

subjects/termeh/statics/moment_of_force_relative_to_center.txt · Ndryshimet e fundit: 2013/07/19 19:53 - ¶

Momenti i një force në lidhje me një pikë përcaktohet nga produkti i modulit të forcës dhe gjatësisë së pingulit të ulur nga pika në vijën e veprimit të forcës (Figura 4).

Figura 4 – Momenti i forcës F në lidhje me pikën O

Kur një trup është i fiksuar në pikën O, forca F tenton ta rrotullojë atë rreth kësaj pike. Pika O rreth së cilës merret momenti quhet qendër e momentit dhe gjatësia e pingules a quhet krahu i forcës në raport me qendrën e momentit.

Momenti i forcës F në raport me O përcaktohet nga produkti i forcës dhe krahut.

M O (F) = F·a.

Momenti konsiderohet pozitiv nëse forca tenton të rrotullojë trupin në drejtim të akrepave të orës, dhe negative - në drejtim të kundërt. Kur vija e veprimit të forcës kalon nëpër një pikë të caktuar, momenti i forcës në lidhje me këtë pikë është i barabartë me zero, pasi në rastin në shqyrtim krahu a = 0 (Figura 5).

Figura 5 – Përcaktimi i shenjës së momentit të forcës në lidhje me një pikë

Ekziston një ndryshim domethënës midis momentit të një çifti dhe momentit të një force. Vlera numerike dhe drejtimi i momentit të një çifti forcash nuk varen nga pozicioni i këtij çifti në rrafsh. Vlera dhe drejtimi (shenja) e momentit të forcës varen nga pozicioni i pikës në lidhje me të cilën përcaktohet momenti.

Ekuacionet e ekuilibrit për një sistem të rrafshët të forcave

Kushtet për ekuilibrin e forcave në një plan: për ekuilibrin e një sistemi forcash të vendosura në mënyrë arbitrare në një rrafsh, është e nevojshme dhe e mjaftueshme që vektori kryesor dhe momenti kryesor i këtyre forcave në lidhje me çdo qendër secili veç e veç të jetë i barabartë me zero. .

F GL = 0; M GL = Σ M O (F i) = 0.

Marrim formën bazë të ekuacionit të ekuilibrit:

Teorikisht, mund të shkruhet një numër i pafund ekuacionesh momentesh, por në praktikë, tre ekuacione ekuilibri janë të mjaftueshme për të zgjidhur problemet në një plan. Në çdo rast specifik, përdoren ekuacione me një të panjohur.

Për raste të ndryshme përdoren tre grupe ekuacionesh ekuilibri:

1. Forma e parë e ekuacioneve të ekuilibrit

2. Forma e dytë e ekuacioneve të ekuilibrit

3. Forma e tretë e ekuacioneve të ekuilibrit

Për një sistem forcash paralele (Figura 43), mund të hartohen vetëm dy ekuacione ekuilibri:

Shembull.

E dhënë: F = 24 kN; q = 6 kN/m; M = 12 kN m α = 60°; a = 1,8 m; b = 5,2 m; c = 3,0 m Përcaktoni reaksionet V A, H A dhe V B (Figura 6).

Figura 6 – Trari i specifikuar me dy mbështetës

I hedhim lidhjet (mbështetësit A ​​dhe B), veprimin e tyre e zëvendësojmë me reaksione: një mbështetje fikse ka reaksione V A (vertikale) dhe H A (horizontale). Mbështetje e lëvizshme - reagimi V B (vertikal). Ne zgjedhim sistemin e koordinatave XY me origjinën në mbështetjen e majtë, përcaktojmë rezultatin e ngarkesës së shpërndarë:

Q = q·a 2 = 6·5,2 = 31,2 kN.

Ne vizatojmë një diagram të projektimit të rrezes (Figura 7).

Figura 7 – Diagrami i projektimit të traut

Për sistemin arbitrar të rrafshit të forcave që rezulton, ne përpilojmë ekuacionet e ekuilibrit:

∑F ix = 0; H A – F cos60° = 0;

∑F i y = 0; V A – F cos30° – Q + V B = 0;

∑М А (F i) = 0; Q·(1,8 + 2,6) + F·cos30°·(1,8 + 5,2) – M – V B ·(1,8 + 5,2 + 3) = 0.

Ne zgjidhim një sistem ekuacionesh.

H A = F cos60° = 24 0,5 = 12 kN;

V A = F cos30° + Q – V B = 24 0,866 + 31,2 – 27,08 = 24,9 kN.

Për të kontrolluar korrektësinë e zgjidhjes, ne përpilojmë shumën e momenteve në lidhje me pikën e aplikimit të forcës së prirur F:

∑М А (F i) = V A ·(1,8 + 5,2) – Q·2,6 – М – V B ·3 = 24,9·7 – 31,2·2,6 – 12 – 27, 08·3 = – 0,06.

Përgjigje: reaksionet mbështetëse të rrezes janë të barabarta me V A = 24,9 kN; V B = 27,08 kN; N A = 12 kN.

Pyetjet e kontrollit:

1. Çfarë e përcakton efektin e një çifti forcash?

2. A varet efekti i një çifti forcash nga pozicioni i tij në rrafsh?

3. A varen vlerat dhe drejtimi i momentit të forcës në lidhje me një pikë nga pozicioni relativ i kësaj pike dhe linja e veprimit të forcës?

4. Kur momenti i një force rreth një pike është i barabartë me zero?

5. Sa ekuacione të pavarura ekuilibri mund të ndërtohen për një sistem të rrafshët të forcave paralele?

E cila është e barabartë me produktin e forcës nga supi i saj.

Momenti i forcës llogaritet duke përdorur formulën:

Ku F- forcë, l- shpatulla e forcës.

Shpatulla e pushtetit- kjo është distanca më e shkurtër nga vija e veprimit të forcës deri te boshti i rrotullimit të trupit. Figura më poshtë tregon një trup të ngurtë që mund të rrotullohet rreth një boshti. Boshti i rrotullimit të këtij trupi është pingul me rrafshin e figurës dhe kalon nëpër pikën, e cila është caktuar si shkronja O. Shpatulla e forcës Ft këtu është distanca l, nga boshti i rrotullimit në vijën e veprimit të forcës. Përcaktohet në këtë mënyrë. Hapi i parë është të vizatoni një vijë veprimi të forcës, pastaj nga pika O, nëpër të cilën kalon boshti i rrotullimit të trupit, ulni një pingul me vijën e veprimit të forcës. Gjatësia e kësaj pingule rezulton të jetë krahu i një force të caktuar.

Momenti i forcës karakterizon veprimin rrotullues të një force. Ky veprim varet si nga forca ashtu edhe nga leva. Sa më i madh të jetë krahu, aq më pak forcë duhet të aplikohet për të marrë rezultatin e dëshiruar, domethënë të njëjtin moment force (shih figurën më lart). Kjo është arsyeja pse është shumë më e vështirë të hapësh një derë duke e shtyrë pranë menteshave sesa duke kapur dorezën dhe është shumë më e lehtë të zhbllokosh një arrë me një çelës të gjatë sesa me një çelës të shkurtër.

Njësia SI e momentit të forcës merret si një moment i forcës prej 1 N, krahu i të cilit është i barabartë me 1 m - njuton metër (N m).

Rregulli i momenteve.

Një trup i ngurtë që mund të rrotullohet rreth një boshti fiks është në ekuilibër nëse momenti i forcës M 1 duke e rrotulluar në drejtim të akrepave të orës është e barabartë me momentin e forcës M 2 , e cila e rrotullon në të kundërt të akrepave të orës:

Rregulli i momenteve është pasojë e një prej teoremave të mekanikës, e cila u formulua nga shkencëtari francez P. Varignon në 1687.

Nja dy forca.

Nëse mbi një trup veprojnë 2 forca të barabarta dhe me drejtim të kundërt që nuk shtrihen në të njëjtën vijë të drejtë, atëherë një trup i tillë nuk është në ekuilibër, pasi momenti rezultues i këtyre forcave në lidhje me çdo bosht nuk është i barabartë me zero. të dyja forcat kanë momente të drejtuara në të njëjtin drejtim . Quhen dy forca të tilla që veprojnë njëkohësisht në një trup nja dy forca. Nëse trupi është i fiksuar në një bosht, atëherë nën veprimin e një palë forcash ai do të rrotullohet. Nëse një trup i lirë zbatohet disa forca, atëherë ai do të rrotullohet rreth boshtit të tij. duke kaluar nëpër qendrën e gravitetit të trupit, figurë b.

Momenti i një çifti forcash është i njëjtë rreth çdo boshti pingul me rrafshin e çiftit. Moment total Mçiftet është gjithmonë e barabartë me produktin e njërës prej forcave F në një distancë l ndërmjet forcave, që quhet shpatullën e çiftit, pa marrë parasysh se cilat segmente l, dhe ndan pozicionin e boshtit të shpatullës së çiftit:

Momenti i disa forcave, rezultantja e të cilave është zero, do të jetë i njëjtë në lidhje me të gjitha boshtet paralele me njëri-tjetrin, prandaj veprimi i të gjitha këtyre forcave në trup mund të zëvendësohet nga veprimi i një çifti forcash me të njëjtën moment.

Kursi bazë i leksioneve për forcën e materialeve, teorinë, praktikën, detyrat.

3.4. Rregulla e shenjës për momentet e përkuljes dhe forcat prerëse.

Forca tërthore në seksionin e rrezes mn (Fig. 3.7, a) konsiderohet pozitive nëse rezultanti i forcave të jashtme në të majtë të seksionit drejtohet nga poshtë lart, dhe në të djathtë - nga lart poshtë, dhe negative - në rastin e kundërt (Fig. 3.7, b).

Momenti i përkuljes në seksionin e rrezes, për shembull në seksionin mn (Fig. 3.8, a), konsiderohet pozitiv nëse momenti rezultues i forcave të jashtme në të majtë të seksionit është i drejtuar në drejtim të akrepave të orës, dhe në të djathtë - në të kundërt dhe negativ. në rastin e kundërt (Fig. 3.8, b). Momentet e paraqitura në Fig. 3.8, a, përkulni traun me konveksitetin e tij poshtë, dhe momentet e paraqitura në Fig. 3.8, b, përkulni traun me konveksitetin e tij lart. Kjo mund të kontrollohet lehtësisht duke përkulur një vizore të hollë.

Kjo nënkupton një rregull tjetër, më të përshtatshëm për t'u mbajtur mend, të shenjave për momentin e përkuljes. Momenti i përkuljes konsiderohet pozitiv nëse në seksionin në shqyrtim trau përkulet në mënyrë konvekse poshtë. Më poshtë do të tregohet se fijet e rrezeve të vendosura në pjesën konkave përjetojnë ngjeshje, dhe në pjesën konvekse, tension. Kështu, duke rënë dakord të vizatojmë ordinatat pozitive të diagramit M lart nga boshti, marrim se diagrami rezulton të jetë i ndërtuar nga ana e fibrave të ngjeshur të rrezes.