Как се определя знакът на момента? Статика. Момент на сила. Основен курс от лекции по съпротивление на материалите, теория, практика, задачи

Инструкции

Нека Q е точката, около която се разглежда моментът на силата. Тази точка се нарича полюс. Начертайте радиус-вектор r от тази точка до точката на прилагане на сила F. Тогава моментът на сила M се определя като векторно произведение на r от F: M=.

Резултатът от кръстосано произведение е вектор. Дължината на вектора се изразява чрез модула: |M|=|r|·|F|·sinφ, където φ е ъгълът между r и F. Векторът M е ортогонален както на вектора r, така и на вектора F: M⊥r , M⊥F.

Векторът M е насочен по такъв начин, че тройката от вектори r, F, M е права. Как да определим, че тройка вектори е правилна? Представете си, че вие ​​(вашето око) сте в края на третия вектор и гледате другите два вектора. Ако изглежда, че най-краткият преход от първия вектор към втория се случва обратно на часовниковата стрелка, това е дясна векторна тройка. В противен случай си имате работа с тройка с лява ръка.

И така, комбинирайте началото на векторите r и F. Това може да стане чрез паралелно прехвърляне на вектора F към точка Q. Сега през същата точка начертайте ос, перпендикулярна на равнината на векторите r и F. Тази ос веднага ще бъде перпендикулярен на векторите. Тук по принцип има само две възможности за насочване на момента на сила: нагоре или надолу.

Опитайте се да насочите момента на сила F нагоре, начертайте векторна стрелка върху оста. От тази стрелка погледнете векторите r и F (можете да използвате символично око). Най-краткият преход от r към F може да бъде обозначен със заоблена стрелка. Правилна ли е тройката от вектори r, F, M? Стрелката сочи ли обратно на часовниковата стрелка? Ако да, значи сте в правилната посока за момента на силата F. Ако не, тогава трябва да промените посоката на противоположната.

Можете също така да определите посоката на момента на силата, като използвате правилото на дясната ръка. Подравнете показалеца си с радиус вектора. Подравнете средния си пръст с вектора на силата. От края на палеца си погледнете двата вектора. Ако преходът от показалеца към средния пръст се извършва обратно на часовниковата стрелка, тогава посоката на момента на силата съвпада с посоката, която сочи палецът. Ако преходът се извършва по посока на часовниковата стрелка, тогава посоката на момента на силата е противоположна на него.

Правилото на гимлета е много подобно на правилото на ръката. С четирите пръста на дясната си ръка завъртете винт от r към F. Векторното произведение ще има посоката, в която е усукана гилбата по време на такова умствено въртене.

Нека сега точка Q се намира на същата права, която съдържа вектора на силата F. Тогава радиус векторът и векторът на силата ще бъдат колинеарни. В този случай тяхното векторно произведение се изражда в нулев вектор и се представя с точка. Нулевият вектор няма специфична посока, но се счита за съпосочен с всеки друг вектор.

За да изчислите правилно ефекта от силата, въртяща тялото, определете точката на нейното приложение и разстоянието от тази точка до оста на въртене. Това е важно за определяне на техническите характеристики на различни механизми. Въртящият момент на двигателя може да се изчисли, ако са известни неговата мощност и скорост.

Ще имаш нужда

• Линийка, динамометър, оборотомер, тестер, тесламетър.

Инструкции

Определете точката или оста, около която тялото. Намерете точката, в която се прилага силата. Свържете точката на прилагане на силата и точката на въртене или спуснете перпендикуляра към оста на въртене. Измерете това разстояние, то е „рамото на силата“. Правете измервания в метри. Измерете силата в нютони с помощта на динамометър. Измерете ъгъла между рамото и вектора на силата. За да изчислите въртящия момент, намерете произведението на силата и синуса на ъгъла между тях M=F r sin(α). Резултатът ще бъде в нютони на метър.

Теоретична механика. Статика:

Система от събиращи се сили
Определение и теорема за трите сили
Графично определение на резултантната на събиращите се сили
Аналитична задача на силата
Аналитично определяне на резултантната на събиращите се сили
Условия и уравнения на равновесие за система от събиращи се сили
Разрешаване на проблем
★ Равновесие под действието на събираща се система от сили

Теория на силовата двойка

Двойка сили и нейните свойства
Теореми за еквивалентност на двойки
Събиране на двойки сили
Равновесие на двойни системи

Привеждане на равнинна система от сили
Лема на Поансо
Теорема за редукция на плоска система от сили
Специални случаи на редукция на равнинна система от сили
Балансирана система от сили

Определяне на опорните реакции на системи с плосък прът
★ Равновесие под действието на система от успоредни сили върху равнина
Паралелна силова система
Произволна плоска система от сили
Произволна плоска система от сили. RGR 1
★ Равновесие на равнинна произволна система от сили
Изчисляване на композитни системи
Изчисляване на композитни системи. RGR 2
★ Равновесие на система от тела 1
★ Равновесие на система от тела 2
★ Равновесие на системата от тела 3
Графично определяне на опорните реакции

субекти:termeh:statics:moment_of_force_relative_to_center

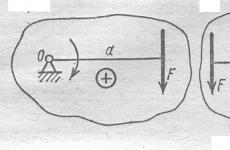
Нека разгледаме тяло, което е фиксирано в центъра O и може да се върти около ос, минаваща през точка O и перпендикулярна на чертожната равнина. Нека приложим сила P в точка А на това тяло и да разберем какво определя въртеливото действие на тази сила ( Фиг. 1).

Очевидно е, че ефектът на силата върху тялото ще зависи не само от нейната величина, но и от това как е насочена и в крайна сметка ще се определя от нейната момент за центъра О.

Определение 1. Моментът на силата P спрямо центъра O е произведението на модула на силата и нейното рамо, взето със знака $\pm$ - тоест дължината на перпендикуляра, спуснат от моментната точка до линията на действие на силата.

Правило за знак: моментът на сила се счита за положителен, ако силата се стреми да върти тялото обратно на часовниковата стрелка и отрицателен, ако върти тялото по посока на часовниковата стрелка.

В съответствие с тази дефиниция моментът на сила е числено равен на двойната площ на триъгълника OAB, конструиран върху вектора на силата P с върха в моментната точка: $M_0(P) = P\cdot d = 2S \Delta_(OAB)$.

Забележи, че моментът на силата спрямо точка O е равен на нула, ако линията на действие на силата минава през моментната точка.

Разгледаното определение на момента на сила е подходящо само за равнинна система от сили. В общия случай, за еднозначно описание на въртеливото действие на сила, въвеждаме следното определение.

Определение 2. Векторът-момент на сила P спрямо центъра O е вектор, който:

приложена в точката на момента O, перпендикулярна на равнината на триъгълник, построен върху вектора на силата с върха в точката на момента;

насочени по правилото на десния винт;

равен по големина на момента на сила P спрямо центъра O (Фиг.1а).

Правило за десен винт, известен също от курсовете по физика като gimlet rule, означава, че ако погледнем към векторния момент $\vec(M_0)(\vec(P))$, ще видим въртенето на равнината на неговото действие от силата $\vec(P)$, протичаща обратно на часовниковата стрелка .

Нека означим с $\vec(r)$ радиус вектора на точката на приложение на силата $\vec(P)$ и докажем, че е вярно следното

Теорема 1. Вектор-момент на сила $\vec(P)$ спрямо центъра ОТНОСНОе равно на векторното произведение на радиус вектора $\vec(r)$ и вектора на силата $\vec(P)$ :

$$\vec(M_0)(\vec(P)) = (\vec(r) \times \vec(P))$$

Спомнете си, че векторното произведение на векторите $\vec(a)\text( и )\vec(b)$ е векторът $\vec(c)$, който ( Фиг.2б):

е перпендикулярна на векторите $\vec(a)\text( и )\vec(b)$ ;

образува с тях дясна тройка вектори, т.е. тя е насочена по такъв начин, че, гледайки към този вектор, ще видим завъртане от вектора $\vec(a)$ към вектора $\vec( b)$ под най-малкия ъгъл, протичащ обратно на часовниковата стрелка;

равен по големина на удвоената площ на триъгълника, изграден върху тези вектори:

$$|\vec(c)| = |\vec(a) \times \vec(b)| = |\vec(a)|\cdot|\vec(b)|\cdot\sin(\vec(a),\,\vec(b))$$

За да докажем теоремата, отбелязваме, първо, че вектор, равен на векторното произведение на векторите $\vec(r)\text( и )\vec(P)$ ще бъде колинеарен на вектора $\vec(M_0) (\vec(P))$ .

За да проверите това, достатъчно е да начертаете тези вектори от една точка ( Фиг.1в). Така $(\vec(r) \times \vec(P)) \uparrow \uparrow \vec(M_0)(\vec(P))$.

Второ, модулът на векторния продукт на тези вектори ще бъде равен на:

$$|\vec(r) \times \vec(P)| = |\vec(r)|\cdot|\vec(P)|\cdot\sin(\vec(r),\,\vec(P)) = P \cdot d =|\vec(M_0)(\ vec(P))|$$

Оттук следва връзката на теоремата.

Следствието от тази теорема е:

Теорема на Вариньон (за момента на резултантната на събиращите се сили). Векторният момент на резултантната система от събиращи се сили спрямо произволен център O е равен на геометричната сума от векторните моменти на всички сили на системата спрямо този център:

$$\vec(M_0)(\vec(R)) = \sum_(i=1)^(i=n)\vec(M_(0\,\,i))(\vec(P_i))$$

Всъщност моментът на резултата, като се вземе предвид Теорема 1и аналитичната дефиниция на резултата от събиращите се сили ще бъде равна на:

$$ \vec(M_0)(\vec(R))= \vec(R)\times\vec(r) \,\,\,\;\;\text( , защото ) \vec(M_0 )(\ vec(P)) = (\vec(r) \times \vec(P)) \\ \vec(R)\times\vec(r)= \vec(r)\times\sum_(i= 1)^ (i=n)\vec(P_i) \,\,\,\;\;\text( , защото ) (\vec(P_1), \vec(P_2), \dots, \vec (P_n)) \sim \vec(R) = \sum_(i=1)^(i=n) \vec(P_i) \\ \vec(r)\times\sum_(i=1)^(i= n)\vec(P_i ) = \sum_(i=1)^(i=n)(\vec(r)\times\vec(P_i)) = \sum_(i=1)^(i=n)\ vec(M_(0\ ,\,i))(\vec(P_i)) $$

За плоска система от сближаващи се сили, геометричната сума в Теорема на Вариньонвлиза в алгебриката:

$$M_0(R)=\sum_(i=1)^(i=n)M_(0\,\,i)(\vec(P_i))$$

Забележка

В образователната литература терминът "момент" се използва за обозначаване както на момент на сила, така и на нейния вектор-момент.

subjects/termeh/statics/moment_of_force_relative_to_center.txt · Последни промени: 2013/07/19 19:53 - ¶

Моментът на сила спрямо точка се определя от произведението на модула на силата и дължината на перпендикуляра, спуснат от точката към линията на действие на силата (Фигура 4).

Фигура 4 – Момент на сила F спрямо точка O

Когато тялото е фиксирано в точка O, силата F се стреми да го завърти около тази точка. Точката O, около която се отчита моментът, се нарича център на момента, а дължината на перпендикуляра a се нарича рамо на силата спрямо центъра на момента.

Моментът на сила F спрямо O се определя от произведението на силата и рамото.

M O (F) = F·a.

Моментът се счита за положителен, ако силата има тенденция да върти тялото по посока на часовниковата стрелка, а отрицателният - обратно на часовниковата стрелка. Когато линията на действие на силата минава през дадена точка, моментът на силата спрямо тази точка е равен на нула, тъй като в разглеждания случай рамото a = 0 (Фигура 5).

Фигура 5 – Определяне на знака на момента на силата спрямо точка

Има една съществена разлика между момента на двойката и момента на силата. Числената стойност и посоката на момента на двойка сили не зависят от позицията на тази двойка в равнината. Стойността и посоката (знакът) на момента на силата зависят от положението на точката, спрямо която се определя моментът.

Уравнения на равновесие за равнинна система от сили

Условия за равновесие на силите в равнина: за равновесие на произволно разположена в равнина система от сили е необходимо и достатъчно главният вектор и главният момент на тези сили спрямо който и да е център поотделно да бъдат равни на нула .

F GL = 0; M GL = Σ M O (F i) = 0.

Получаваме основната форма на уравнението на равновесието:

Теоретично могат да се напишат безкраен брой моментни уравнения, но на практика три уравнения на равновесие са достатъчни за решаване на задачи в равнина. Във всеки конкретен случай се използват уравнения с едно неизвестно.

За различни случаи се използват три групи уравнения на равновесие:

1. Първа форма на уравненията на равновесието

2. Втора форма на уравненията на равновесието

3. Трета форма на уравненията на равновесието

За система от успоредни сили (Фигура 43) могат да се съставят само две уравнения на равновесие:

Пример.

дадени: F = 24 kN; q = 6 kN/m; M = 12 kN m α = 60°; а = 1,8 m; b = 5,2 m; c = 3,0 м. Определете реакциите V A, H A и V B (Фигура 6).

Фигура 6 – Специфицирана двуподпорна греда

Изхвърляме връзките (опори A и B), заменяме тяхното действие с реакции: неподвижната опора има реакции V A (вертикално) и H A (хоризонтално). Подвижна опора - реакция V B (вертикална). Избираме координатната система XY с начало в лявата опора, определяме резултата от разпределеното натоварване:

Q = q·a 2 = 6·5,2 = 31,2 kN.

Начертаваме проектна диаграма на гредата (Фигура 7).

Фигура 7 – Проектна схема на гредата

За получената произволна равнинна система от сили съставяме уравненията на равновесието:

∑F ix = 0; H A – F cos60° = 0;

∑F i y = 0; V A – F cos30° – Q + V B = 0;

∑М А (F i) = 0; Q·(1,8 + 2,6) + F·cos30°·(1,8 + 5,2) – M – V B ·(1,8 + 5,2 + 3) = 0.

Решаваме система от уравнения.

H A = F cos60° = 24 0,5 = 12 kN;

V A = F cos30° + Q – V B = 24 0,866 + 31,2 – 27,08 = 24,9 kN.

За да проверим правилността на решението, съставяме сумата от моментите спрямо точката на приложение на наклонената сила F:

∑М А (F i) = V A ·(1,8 + 5,2) – Q·2,6 – М – V B ·3 = 24,9·7 – 31,2·2,6 – 12 – 27, 08·3 = – 0,06.

Отговор: опорните реакции на гредата са равни на V A = 24,9 kN; V B = 27,08 kN; N A = 12 kN.

Контролни въпроси:

1. Какво определя ефекта на двойка сили?

2. Ефектът на двойка сили зависи ли от нейното положение в равнината?

3. Зависят ли стойностите и посоката на момента на сила спрямо точка от относителното положение на тази точка и линията на действие на силата?

4. Кога моментът на сила спрямо точка е равен на нула?

5. Колко независими уравнения на равновесие могат да бъдат съставени за равнинна система от успоредни сили?

Което е равно на произведението на силата от нейното рамо.

Моментът на силата се изчислява по формулата:

Където Е- сила, л- рамо на силата.

Рамо на властта- това е най-късото разстояние от линията на действие на силата до оста на въртене на тялото. Фигурата по-долу показва твърдо тяло, което може да се върти около ос. Оста на въртене на това тяло е перпендикулярна на равнината на фигурата и минава през точката, която е обозначена с буквата О. Рамото на силата Ftето разстоянието л, от оста на въртене до линията на действие на силата. Дефинира се така. Първата стъпка е да начертаете линия на действие на силата, след което от точка О, през която минава оста на въртене на тялото, спуснете перпендикуляр към линията на действие на силата. Дължината на този перпендикуляр се оказва рамото на дадена сила.

Силовият момент характеризира въртеливото действие на силата. Това действие зависи както от силата, така и от ливъриджа. Колкото по-голямо е рамото, толкова по-малка сила трябва да се приложи, за да се получи желаният резултат, тоест същия момент на сила (вижте фигурата по-горе). Ето защо е много по-трудно да отворите врата, като я натиснете близо до пантите, отколкото като хванете дръжката, и е много по-лесно да развиете гайка с дълъг, отколкото с къс гаечен ключ.

Единицата SI за момент на сила се приема за момент на сила от 1 N, чието рамо е равно на 1 m - нютон метър (N m).

Правило на моментите.

Твърдо тяло, което може да се върти около фиксирана ос, е в равновесие, ако моментът на сила М 1въртенето му по посока на часовниковата стрелка е равно на момента на силата М 2 , което го завърта обратно на часовниковата стрелка:

Правилото на моментите е следствие от една от теоремите на механиката, която е формулирана от френския учен П. Вариньон през 1687 г.

Няколко сили.

Ако върху едно тяло действат 2 равни и противоположно насочени сили, които не лежат на една и съща права линия, тогава такова тяло не е в равновесие, тъй като резултантният момент на тези сили спрямо която и да е ос не е равен на нула, тъй като и двете сили имат моменти, насочени в една и съща посока. Две такива сили, действащи едновременно върху тялото, се наричат няколко сили. Ако тялото е фиксирано върху ос, тогава под действието на двойка сили то ще се върти. Ако върху свободно тяло се приложат няколко сили, то ще се върти около оста си. преминаващ през центъра на тежестта на тялото, фигура b.

Моментът на двойка сили е еднакъв за всяка ос, перпендикулярна на равнината на двойката. Тотален момент Мдвойки винаги е равна на произведението на една от силите Ена разстояние лмежду силите, което се нарича рамото на двойката, без значение какви сегменти л, и споделя позицията на оста на рамото на двойката:

Моментът на няколко сили, чийто резултат е нула, ще бъде еднакъв спрямо всички успоредни една на друга оси, следователно действието на всички тези сили върху тялото може да бъде заменено с действието на една двойка сили със същото момент.

Основен курс от лекции по съпротивление на материалите, теория, практика, задачи.

3.4. Правило за знак за огъващи моменти и срязващи сили.

Напречната сила в сечението на гредата mn (фиг. 3.7, а) се счита за положителна, ако резултатът от външните сили отляво на сечението е насочен отдолу нагоре, а отдясно - отгоре надолу, и отрицателен - в обратния случай (фиг. 3.7, б).

Моментът на огъване в сечение на лъча, например в сечение mn (фиг. 3.8, а), се счита за положителен, ако резултантният момент на външните сили вляво от сечението е насочен по посока на часовниковата стрелка, а вдясно - обратно на часовниковата стрелка, и отрицателен в обратния случай (фиг. 3.8 , b). Моментите, показани на фиг. 3.8, а, огънете гредата с нейната изпъкналост надолу и моментите, показани на фиг. 3.8, b, огънете гредата с нейната изпъкналост нагоре. Това може лесно да се провери чрез огъване на тънка линийка.

Това предполага друго, по-удобно за запомняне, правило за знаци за момента на огъване. Моментът на огъване се счита за положителен, ако в разглеждания участък лъчът се огъва изпъкнало надолу. По-долу ще бъде показано, че влакната на лъча, разположени във вдлъбната част, изпитват компресия, а в изпъкналата част - напрежение. По този начин, съгласявайки се да начертаем положителните ординати на диаграмата M нагоре от оста, получаваме, че диаграмата се оказва изградена от страната на компресираните влакна на лъча.