Jak określa się znak chwili? Statyka. Chwila mocy. Podstawowy kurs wykładów z wytrzymałości materiałów, teorii, praktyki, zadań

Instrukcje

Niech Q będzie punktem, względem którego rozważany jest moment siły. Ten punkt nazywa się biegunem. Narysuj wektor promienia r od tego punktu do punktu przyłożenia siły F. Następnie moment siły M definiuje się jako iloczyn wektorowy r przez F: M=.

Wynikiem iloczynu krzyżowego jest wektor. Długość wektora wyraża się modułem: |M|=|r|·|F|·sinφ, gdzie φ jest kątem pomiędzy r i F. Wektor M jest ortogonalny zarówno do wektora r, jak i wektora F: M⊥r , M⊥F.

Wektor M jest skierowany w taki sposób, że trójka wektorów r, F, M jest właściwa. Jak ustalić, że trójka wektorów jest poprawna? Wyobraź sobie, że ty (twoje oko) znajdujesz się na końcu trzeciego wektora i patrzysz na dwa pozostałe wektory. Jeśli wydaje się, że najkrótsze przejście od pierwszego wektora do drugiego następuje w kierunku przeciwnym do ruchu wskazówek zegara, jest to trójka wektora prawoskrętnego. W przeciwnym razie masz do czynienia z leworęczną trójką.

Zatem połączmy początki wektorów r i F. Można to zrobić poprzez równoległe przeniesienie wektora F do punktu Q. Teraz przez ten sam punkt narysuj oś prostopadłą do płaszczyzny wektorów r i F. Oś ta będzie natychmiast prostopadła do wektorów. Tutaj w zasadzie istnieją tylko dwie możliwości skierowania momentu siły: w górę lub w dół.

Spróbuj skierować moment siły F w górę, narysuj strzałkę wektorową na osi. Z tej strzałki spójrz na wektory r i F (możesz użyć symbolicznego oka). Najkrótsze przejście od r do F można oznaczyć zaokrągloną strzałką. Czy trójka wektorów r, F, M jest poprawna? Czy strzałka jest skierowana w kierunku przeciwnym do ruchu wskazówek zegara? Jeśli tak, to jesteś we właściwym kierunku dla momentu siły F. Jeśli nie, to musisz zmienić kierunek na przeciwny.

Kierunek momentu siły można również określić, korzystając z reguły prawej ręki. Dopasuj palec wskazujący do wektora promienia. Wyrównaj środkowy palec z wektorem siły. Patrząc z końca kciuka na dwa wektory. Jeśli przejście od palca wskazującego do środkowego odbywa się w kierunku przeciwnym do ruchu wskazówek zegara, wówczas kierunek momentu siły pokrywa się z kierunkiem wskazanym kciukiem. Jeśli przejście następuje zgodnie z ruchem wskazówek zegara, wówczas kierunek momentu siły jest przeciwny do niego.

Reguła świdra jest bardzo podobna do reguły ręki. Czterema palcami prawej ręki obróć śrubę od r do F. Iloczyn wektorowy będzie miał kierunek, w którym świder jest skręcony podczas takiego obrotu mentalnego.

Niech teraz punkt Q będzie leżał na tej samej prostej, która zawiera wektor siły F. Wtedy wektor promienia i wektor siły będą współliniowe. W tym przypadku ich iloczyn wektorowy degeneruje się do wektora zerowego i jest reprezentowany przez punkt. Wektor zerowy nie ma określonego kierunku, ale jest uważany za współkierunkowy z dowolnym innym wektorem.

Aby poprawnie obliczyć działanie siły obracającej ciało, należy określić punkt jej przyłożenia oraz odległość tego punktu od osi obrotu. Jest to ważne przy określaniu właściwości technicznych różnych mechanizmów. Moment obrotowy silnika można obliczyć, znając jego moc i prędkość.

Będziesz potrzebować

• Linijka, dynamometr, obrotomierz, tester, teslametr.

Instrukcje

Określ punkt lub oś, wokół której znajduje się ciało. Znajdź punkt, w którym przyłożona jest siła. Połącz punkt przyłożenia siły z punktem obrotu lub opuść prostopadle do osi obrotu. Zmierz tę odległość, jest to „ramię siły”. Dokonuj pomiarów w metrach. Zmierz siłę w niutonach za pomocą dynamometru. Zmierz kąt pomiędzy ramieniem a wektorem siły. Aby obliczyć moment obrotowy, znajdź iloczyn siły i sinus kąta między nimi M=F r sin(α). Wynik będzie w niutonach na metr.

Mechanika teoretyczna. Statyka:

Układ zbiegających się sił
Definicja i twierdzenie o trzech siłach
Graficzne określenie wypadkowej sił zbiegających się
Analityczne zadanie siły
Analityczne wyznaczanie wypadkowej sił zbiegających się
Warunki i równania równowagi układu sił zbieżnych
Rozwiązywanie problemów
★ Równowaga pod działaniem zbieżnego układu sił

Teoria pary siłowej

Para sił i jej właściwości
Twierdzenia o równoważności par
Dodawanie par sił
Równowaga układów par

Doprowadzenie do płaskiego układu sił
Lemat Poinsota
Twierdzenie o redukcji płaskiego układu sił
Szczególne przypadki redukcji płaskiego układu sił
Zrównoważony układ sił

Wyznaczanie reakcji podporowych układów prętów płaskich
★ Równowaga pod działaniem układu sił równoległych na płaszczyźnie
Układ sił równoległych
Dowolny płaski układ sił
Dowolny płaski układ sił. RGR 1
★ Równowaga płaskiego dowolnego układu sił
Obliczanie układów złożonych
Obliczanie układów złożonych. RGR 2
★ Równowaga układu ciał 1
★ Równowaga układu ciał 2
★ Równowaga układu ciał 3
Graficzne wyznaczanie reakcji podporowych

topics:termeh:statics:moment_of_force_relative_to_center

Rozważmy bryłę, która jest zamocowana w środku O i może obracać się wokół osi przechodzącej przez punkt O i prostopadłej do płaszczyzny rysunku. Przyłóżmy siłę P w punkcie A tego ciała i dowiedzmy się, co decyduje o działaniu obrotowym tej siły ( Ryc.1).

Jest oczywiste, że wpływ siły na ciało będzie zależał nie tylko od jej wielkości, ale także od sposobu jej skierowania i ostatecznie będzie określony przez jej moment wokół środka O.

Definicja 1. Moment siły P względem środka O jest iloczynem modułu siły i jej ramienia przyjętego ze znakiem $\pm$ - czyli długości prostopadłej obniżonej od punktu momentu do prostej działania siły.

Zasada znaku: moment siły uważa się za dodatni, jeśli siła ma tendencję do obracania ciała w kierunku przeciwnym do ruchu wskazówek zegara, i za ujemny, jeśli obraca ciało w kierunku zgodnym z ruchem wskazówek zegara.

Zgodnie z tą definicją moment siły jest liczbowo równy podwójnemu polu trójkąta OAB, zbudowanego na wektorze siły P z wierzchołkiem w punkcie chwili: $M_0(P) = P\cdot d = 2S \Delta_(OAB)$ .

Zauważ to moment siły względem punktu O jest równy zeru, jeśli linia działania siły przechodzi przez punkt momentu.

Rozważana definicja momentu siły jest odpowiednia tylko dla płaskiego układu sił. W ogólnym przypadku, aby jednoznacznie opisać obrotowe działanie siły, wprowadzamy następującą definicję.

Definicja 2. Moment wektorowy siły P względem środka O jest wektorem, który:

przyłożony w momencie punktu O prostopadle do płaszczyzny trójkąta zbudowanego na wektorze siły z wierzchołkiem w punkcie momentu;

kierowane zgodnie z zasadą prawej śruby;

równy momentowi siły P względem środka O (Ryc.1a).

Reguła prawej śruby, znany również z zajęć z fizyki jako zasada świdra, oznacza, że ​​patrząc w stronę momentu wektorowego $\vec(M_0)(\vec(P))$ , zobaczymy obrót płaszczyzny jego działania przez siłę $\vec(P)$, występujący w kierunku przeciwnym do ruchu wskazówek zegara .

Oznaczmy przez $\vec(r)$ wektor promienia punktu przyłożenia siły $\vec(P)$ i udowodnijmy, że prawdziwe jest poniższe

Twierdzenie 1. Wektor-moment siły $\vec(P)$ względem środka O jest równy iloczynowi wektora promienia $\vec(r)$ i wektora siły $\vec(P)$ :

$$\vec(M_0)(\vec(P)) = (\vec(r) \times \vec(P))$$

Przypomnijmy, że iloczyn wektorowy wektorów $\vec(a)\text( i )\vec(b)$ to wektor $\vec(c)$ , który ( Ryc.2b):

jest prostopadła do wektorów $\vec(a)\text( i )\vec(b)$ ;

tworzy z nimi prawostronną trójkę wektorów, czyli jest ona skierowana w ten sposób, że patrząc w stronę tego wektora zobaczymy obrót od wektora $\vec(a)$ do wektora $\vec( b)$ pod najmniejszym kątem, występującym w kierunku przeciwnym do ruchu wskazówek zegara;

równy pod względem wielkości dwukrotnej powierzchni trójkąta zbudowanego na tych wektorach:

$$|\vec(c)| = |\vec(a) \times \vec(b)| = |\vec(a)|\cdot|\vec(b)|\cdot\sin(\vec(a),\,\vec(b))$$

Aby udowodnić twierdzenie, zauważamy najpierw, że wektor równy iloczynowi wektorowemu wektorów $\vec(r)\text( i )\vec(P)$ będzie współliniowy z wektorem $\vec(M_0) (\vec(P))$ .

Aby to sprawdzić, wystarczy wykreślić te wektory z jednego punktu ( Ryc.1c). Zatem $(\vec(r) \times \vec(P)) \uparrow \uparrow \vec(M_0)(\vec(P))$.

Po drugie, moduł iloczynu wektorowego tych wektorów będzie równy:

$$|\vec(r) \times \vec(P)| = |\vec(r)|\cdot|\vec(P)|\cdot\sin(\vec(r),\,\vec(P)) = P \cdot d =|\vec(M_0)(\ vec(P))|$$

W tym miejscu następuje relacja twierdzenia.

Konsekwencją tego twierdzenia jest:

Twierdzenie Varignona (o momencie wypadkowej sił zbiegających się). Moment wektorowy wypadkowego układu zbieżnych sił względem dowolnego środka O jest równy sumie geometrycznej momentów wektorowych wszystkich sił układu względem tego środka:

$$\vec(M_0)(\vec(R)) = \sum_(i=1)^(i=n)\vec(M_(0\,\,i))(\vec(P_i))$$

W rzeczywistości moment wynikowy, biorąc pod uwagę Twierdzenie 1 a analityczna definicja wypadkowej sił zbieżnych będzie równa:

$$ \vec(M_0)(\vec(R))= \vec(R)\times\vec(r) \,\,\,\;\;\text( , ponieważ ) \vec(M_0 )(\ vec(P)) = (\vec(r) \times \vec(P)) \\ \vec(R)\times\vec(r)= \vec(r)\times\sum_(i= 1)^ (i=n)\vec(P_i) \,\,\,\;\;\text( , ponieważ ) (\vec(P_1), \vec(P_2), \dots, \vec (P_n)) \sim \vec(R) = \sum_(i=1)^(i=n) \vec(P_i) \\ \vec(r)\times\sum_(i=1)^(i= n)\vec(P_i ) = \sum_(i=1)^(i=n)(\vec(r)\times\vec(P_i)) = \sum_(i=1)^(i=n)\ vec(M_(0\ ,\,i))(\vec(P_i)) $$

W przypadku płaskiego układu zbieżnych sił suma geometryczna wynosi Twierdzenie Varignona przechodzi do algebraicznego:

$$M_0(R)=\suma_(i=1)^(i=n)M_(0\,\,i)(\vec(P_i))$$

Notatka

W literaturze edukacyjnej termin „moment” używany jest do określenia zarówno momentu siły, jak i jej momentu wektorowego.

topics/termeh/statics/moment_of_force_relative_to_center.txt · Ostatnie zmiany: 2013/07/19 19:53 - ¶

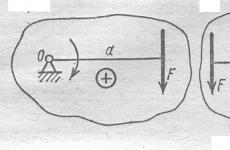
Moment siły względem punktu wyznacza się jako iloczyn modułu siły i długości prostopadłej opuszczonej z punktu do linii działania siły (rysunek 4).

Rysunek 4 – Moment siły F względem punktu O

Kiedy ciało jest zamocowane w punkcie O, siła F ma tendencję do obracania go wokół tego punktu. Punkt O, wokół którego mierzony jest moment, nazywany jest środkiem momentu, a długość prostopadłej a nazywana jest ramieniem siły względem środka momentu.

Moment siły F względem O jest określony przez iloczyn siły i ramienia.

M O (F) = F·a.

Moment uważa się za dodatni, jeśli siła ma tendencję do obracania ciała w kierunku zgodnym z ruchem wskazówek zegara, a ujemna - w kierunku przeciwnym do ruchu wskazówek zegara. Gdy linia działania siły przechodzi przez dany punkt, moment siły względem tego punktu jest równy zeru, gdyż w rozpatrywanym przypadku ramię a = 0 (rysunek 5).

Rysunek 5 – Wyznaczanie znaku momentu siły względem punktu

Istnieje jedna istotna różnica pomiędzy momentem pary a momentem siły. Wartość liczbowa i kierunek momentu pary sił nie zależą od położenia tej pary w płaszczyźnie. Wartość i kierunek (znak) momentu siły zależą od położenia punktu, względem którego wyznaczany jest moment.

Równania równowagi dla płaskiego układu sił

Warunki równowagi sił na płaszczyźnie: dla równowagi układu sił dowolnie rozmieszczonych na płaszczyźnie konieczne i wystarczające jest, aby wektor główny i moment główny tych sił względem dowolnego środka były z osobna równe zeru .

FGL = 0; M GL = Σ M O (F i) = 0.

Otrzymujemy podstawową postać równania równowagi:

Teoretycznie można zapisać nieskończoną liczbę równań momentów, ale w praktyce do rozwiązania problemów na płaszczyźnie wystarczą trzy równania równowagi. W każdym konkretnym przypadku stosuje się równania z jedną niewiadomą.

Dla różnych przypadków stosuje się trzy grupy równań równowagi:

1. Pierwsza postać równań równowagi

2. Druga postać równań równowagi

3. Trzecia postać równań równowagi

Dla układu sił równoległych (Rysunek 43) można sporządzić tylko dwa równania równowagi:

Przykład.

Dany: F = 24 kN; q = 6 kN/m; M = 12 kN m α = 60°; a = 1,8 m; b = 5,2 m; c = 3,0 m. Określ reakcje V A, H A i V B (rysunek 6).

Rysunek 6 – Określona belka dwupodporowa

Odrzucamy połączenia (podpory A i B), zastępujemy ich działanie reakcjami: podpora nieruchoma ma reakcje V A (pionowe) i H A (poziome). Podpora ruchoma - reakcja V B (pionowa). Wybieramy układ współrzędnych XY z początkiem w lewej podporze, wyznaczamy wypadkową obciążenia rozłożonego:

Q = q·a 2 = 6·5,2 = 31,2 kN.

Rysujemy schemat konstrukcyjny belki (ryc. 7).

Rysunek 7 – Schemat konstrukcyjny belki

Dla powstałego dowolnego płaskiego układu sił układamy równania równowagi:

∑F ix = 0; H A – F cos60° = 0;

∑F i y = 0; V A – F cos30° – Q + V B = 0;

∑М А (F i) = 0; Q·(1,8 + 2,6) + F·cos30°·(1,8 + 5,2) – M – V B ·(1,8 + 5,2 + 3) = 0.

Rozwiązujemy układ równań.

H A = F cos60° = 24 0,5 = 12 kN;

V A = F cos30° + Q – V B = 24 0,866 + 31,2 – 27,08 = 24,9 kN.

Aby sprawdzić poprawność rozwiązania, zestawiamy sumę momentów względem punktu przyłożenia siły ukośnej F:

∑М А (F i) = V A·(1,8 + 5,2) – Q·2,6 – М – V B ·3 = 24,9,7 – 31,2·2,6 – 12 – 27, 08,3 = – 0,06.

Odpowiedź: reakcje podporowe belki są równe VA = 24,9 kN; V B = 27,08 kN; N A = 12 kN.

Pytania kontrolne:

1. Co decyduje o działaniu pary sił?

2. Czy działanie pary sił zależy od jej położenia w płaszczyźnie?

3. Czy wartości i kierunek momentu siły względem punktu zależą od względnego położenia tego punktu i linii działania siły?

4. Kiedy moment siły względem punktu jest równy zeru?

5. Ile niezależnych równań równowagi można zbudować dla płaskiego układu sił równoległych?

Co jest równe iloczynowi siły działającej na jego ramię.

Moment siły oblicza się ze wzoru:

Gdzie F- siła, l- ramię siły.

Ramię mocy- jest to najkrótsza odległość od linii działania siły do ​​osi obrotu ciała. Poniższy rysunek przedstawia sztywny korpus, który może obracać się wokół osi. Oś obrotu tego ciała jest prostopadła do płaszczyzny figury i przechodzi przez punkt oznaczony literą O. Ramię siły Ft oto odległość l, od osi obrotu do linii działania siły. Definiuje się to w ten sposób. Pierwszym krokiem jest narysowanie linii działania siły, następnie z punktu O, przez który przechodzi oś obrotu ciała, obniż prostopadle do linii działania siły. Długość tej prostopadłej okazuje się być ramieniem danej siły.

Moment siły charakteryzuje obrotowe działanie siły. To działanie zależy zarówno od siły, jak i dźwigni. Im większe ramię, tym mniejszą siłę należy przyłożyć, aby uzyskać pożądany efekt, czyli ten sam moment siły (patrz rysunek powyżej). Dlatego znacznie trudniej otworzyć drzwi, dociskając je w pobliże zawiasów, niż chwytając za klamkę, a o wiele łatwiej odkręcić nakrętkę długim kluczem niż krótkim.

Za jednostkę momentu siły w układzie SI przyjmuje się moment siły 1 N, którego ramię jest równe 1 m - niutonometr (N m).

Zasada momentów.

Ciało sztywne, które może obracać się wokół ustalonej osi, znajduje się w równowadze, jeśli moment siły M 1 obrót go w kierunku zgodnym z ruchem wskazówek zegara jest równy momentowi siły M 2 , który obraca go w kierunku przeciwnym do ruchu wskazówek zegara:

Reguła momentów jest konsekwencją jednego z twierdzeń mechaniki, które sformułował francuski naukowiec P. Varignon w 1687 roku.

Parę sił.

Jeżeli na ciało działają 2 równe i przeciwnie skierowane siły, które nie leżą na tej samej prostej, to ciało takie nie jest w równowadze, gdyż wypadkowy moment tych sił względem dowolnej osi nie jest równy zeru, gdyż obie siły mają momenty skierowane w tym samym kierunku. Dwie takie siły działające jednocześnie na ciało nazywamy parę sił. Jeśli ciało jest zamocowane na osi, to pod działaniem pary sił będzie się obracać. Jeśli na wolne ciało przyłoży się kilka sił, wówczas obróci się ono wokół własnej osi. przechodząc przez środek ciężkości ciała, figura B.

Moment pary sił jest taki sam względem dowolnej osi prostopadłej do płaszczyzny pary. Całkowita chwila M par jest zawsze równa iloczynowi jednej z sił F na odległość l pomiędzy siłami, tzw ramię pary, bez względu na segmenty l, i dzieli położenie osi ramienia pary:

Moment kilku sił, których wypadkowa wynosi zero, będzie taki sam względem wszystkich osi równoległych do siebie, dlatego działanie wszystkich tych sił na ciało można zastąpić działaniem jednej pary sił o tych samych za chwilę.

Podstawowy kurs wykładów z wytrzymałości materiałów, teorii, praktyki, zadań.

3.4. Reguła znaku dla momentów zginających i sił ścinających.

Siłę poprzeczną w przekroju belki mn (ryc. 3.7, a) uważa się za dodatnią, jeżeli wypadkowa sił zewnętrznych po lewej stronie przekroju jest skierowana od dołu do góry, a po prawej stronie - od góry do dołu, oraz negatywny - w odwrotnym przypadku (ryc. 3.7, b).

Moment zginający w przekroju belki, na przykład w przekroju mn (ryc. 3.8, a), uważa się za dodatni, jeśli wypadkowy moment sił zewnętrznych po lewej stronie przekroju jest skierowany zgodnie z ruchem wskazówek zegara, a po prawej - przeciwnie do ruchu wskazówek zegara i ujemny w przeciwnym przypadku (ryc. 3.8 , b). Momenty pokazane na rys. 3.8, a, zagnij belkę wypukłością w dół, a momenty pokazane na ryc. 3.8, b, zagnij belkę wypukłością do góry. Można to łatwo sprawdzić, wyginając cienką linijkę.

Oznacza to inną, wygodniejszą do zapamiętania zasadę znaków momentu zginającego. Moment zginający uważa się za dodatni, jeśli w rozpatrywanym przekroju belka wygina się wypukłie w dół. Poniżej zostanie pokazane, że włókna belki znajdujące się w części wklęsłej podlegają ściskaniu, a w części wypukłej rozciąganiu. Zatem zgadzając się na wykreślenie dodatnich rzędnych wykresu M w górę od osi, otrzymujemy, że wykres okazuje się być zbudowany od strony ściśniętych włókien belki.