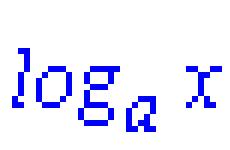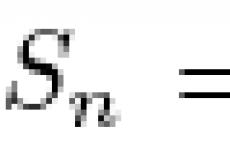Construcție Snowflake Koch. Fractali fulgi de nea Koch. Definiția terminologiei „fractali”

Această cifră este unul dintre primii fractali studiati de oamenii de știință. Este derivat din trei copii ale curbei Koch, care a apărut pentru prima dată într-o lucrare a matematicianului suedez Helge von Koch în 1904. Această curbă a fost inventată ca exemplu de linie continuă care nu poate fi tangentă la niciun punct. Liniile cu această proprietate erau cunoscute înainte (Karl Weierstrass și-a construit exemplul în 1872), dar curba Koch este remarcabilă prin simplitatea designului său. Nu este o coincidență faptul că articolul său se numește „Pe o curbă continuă fără tangente, care rezultă din geometria elementară”.

Cum se construiește curba Koch pas cu pas.

Prima iterație este pur și simplu segmentul inițial. Apoi este împărțit în trei părți egale, cea centrală este completată pentru a forma un triunghi regulat și apoi aruncată. Rezultatul este a doua iterație - o linie întreruptă formată din patru segmente. La fiecare dintre ele se aplică aceeași operațiune și se obține a patra etapă de construcție. Continuând în același spirit, puteți obține din ce în ce mai multe linii noi (toate vor fi linii întrerupte). Iar ceea ce se întâmplă în limită (acesta va fi deja un obiect imaginar) se numește curba Koch.

Proprietățile de bază ale curbei Koch

1.O este continuu, dar nu poate fi diferentiat nicaieri. În linii mari, tocmai acesta este motivul pentru care a fost inventat - ca exemplu al acestui tip de „ciudați” matematici.

2. Are lungime infinită. Fie lungimea segmentului inițial egală cu 1. La fiecare pas de construcție înlocuim fiecare dintre segmentele care alcătuiesc linia cu o linie întreruptă, care 4/3 ori mai mult. Aceasta înseamnă că lungimea întregii linii întrerupte la fiecare pas este înmulțită cu 4/3 : lungimea liniei numărul n este (4/3)n–1. Prin urmare, linia limită nu are de ales decât să fie infinit de lungă.

3. Fulgul lui Koch limitează aria finită. Și asta în ciuda faptului că perimetrul său este infinit. Această proprietate poate părea paradoxală, dar este evidentă - un fulg de zăpadă se potrivește complet într-un cerc, așa că aria sa este evident limitată. Aria poate fi calculată și nici măcar nu aveți nevoie de cunoștințe speciale pentru aceasta - formulele pentru aria unui triunghi și suma unei progresii geometrice sunt predate la școală. Pentru cei interesați, calculul este listat mai jos cu litere mici.

Fie latura triunghiului regulat original egal cu a. Apoi zona sa. Mai întâi latura este 1 și aria este: . Ce se întâmplă pe măsură ce iterația crește? Putem presupune că mici triunghiuri echilaterale sunt atașate unui poligon existent. Prima dată sunt doar 3, iar de fiecare dată sunt de 4 ori mai mulți decât precedentul. Adică la al n-lea pas va fi finalizat Tn = 3 4n–1 triunghiuri. Lungimea laturii fiecăreia dintre ele este o treime din latura triunghiului completat în pasul anterior. Aceasta înseamnă că este egal cu (1/3)n. Arii sunt proporționale cu pătratele laturilor, deci aria fiecărui triunghi este . Pentru valorile mari ale lui n, acesta este, apropo, foarte mic. Contribuția totală a acestor triunghiuri la zona fulgului de nea este Tn Sn = 3/4 (4/9)n S0. Prin urmare, după al n-lea pas, aria figurii va fi egală cu suma S0 + T1 S1 + T2 S2 + ... +Tn Sn = . Un fulg de zăpadă se obține după un număr infinit de pași, care îi corespunde n → ∞. Rezultatul este o sumă infinită, dar aceasta este suma unei progresii geometrice descrescătoare; există o formulă pentru aceasta: . Zona fulgului de nea este .

Opțiuni pentru construirea fulgului de zăpadă Koch

Fulgul de zăpadă Koch „dimpotrivă” se obține dacă construim curbe Koch în interiorul triunghiului echilateral original.

replici Cesaro. În loc de triunghiuri echilaterale, se folosesc triunghiuri isoscele cu un unghi de bază de la 60° la 90°. În figură, unghiul este de 88°.

Opțiune pătrată. Aici pătratele sunt completate.

Trei copii ale curbei Koch, construite (cu punctele lor spre exterior) pe laturile unui triunghi regulat, formează o curbă închisă de lungime infinită numită fulgul de nea lui Koch.

Această cifră este unul dintre primii fractali studiati de oamenii de știință. Vine din trei exemplare curba Koch, care a apărut pentru prima dată într-o lucrare a matematicianului suedez Helge von Koch în 1904. Această curbă a fost inventată ca exemplu de linie continuă care nu poate fi tangentă la niciun punct. Liniile cu această proprietate erau cunoscute înainte (Karl Weierstrass și-a construit exemplul în 1872), dar curba Koch este remarcabilă prin simplitatea designului său. Nu este o coincidență faptul că articolul său se numește „Pe o curbă continuă fără tangente, care rezultă din geometria elementară”.

Desenul și animația arată perfect cum este construită curba Koch pas cu pas. Prima iterație este pur și simplu segmentul inițial. Apoi este împărțit în trei părți egale, cea centrală este completată pentru a forma un triunghi regulat și apoi aruncată. Rezultatul este a doua iterație - o linie întreruptă formată din patru segmente. La fiecare dintre ele se aplică aceeași operațiune și se obține a patra etapă de construcție. Continuând în același spirit, puteți obține din ce în ce mai multe linii noi (toate vor fi linii întrerupte). Iar ceea ce se întâmplă în limită (acesta va fi deja un obiect imaginar) se numește curba Koch.

Proprietățile de bază ale curbei Koch

1. Este continuu, dar nicaieri diferentiabil. În linii mari, tocmai acesta este motivul pentru care a fost inventat - ca exemplu al acestui tip de „ciudați” matematici.

2. Are lungime infinită. Fie lungimea segmentului inițial egală cu 1. La fiecare pas de construcție înlocuim fiecare dintre segmentele care alcătuiesc linia cu o linie întreruptă, care este de 4/3 ori mai lungă. Aceasta înseamnă că lungimea întregii linii întrerupte este înmulțită cu 4/3 la fiecare pas: lungimea liniei cu număr n egal cu (4/3) n-1 . Prin urmare, linia limită nu are de ales decât să fie infinit de lungă.

Fie latura triunghiului regulat original egal cu A. Atunci aria sa este . Mai întâi latura este 1 și aria este: . Ce se întâmplă pe măsură ce iterația crește? Putem presupune că mici triunghiuri echilaterale sunt atașate unui poligon existent. Prima dată sunt doar 3, iar de fiecare dată sunt de 4 ori mai mulți decât precedentul. Adică pe n al treilea pas va fi finalizat Tn= 3 4 n-1 triunghiuri. Lungimea laturii fiecăreia dintre ele este o treime din latura triunghiului completat în pasul anterior. Deci este egal cu (1/3) n. Arii sunt proporționale cu pătratele laturilor, deci aria fiecărui triunghi este . Pentru valori mari n Apropo, acest lucru este foarte puțin. Contribuția totală a acestor triunghiuri la zona fulgului de nea este Tn · S n= 3/4 · (4/9) n · S 0 . Prin urmare după n-pas, aria figurii va fi egală cu suma S 0 + T 1 · S 1 + T 2 · S 2 + ... +Tn S n = . Un fulg de zăpadă se obține după un număr infinit de pași, care îi corespunde n→ ∞. Rezultatul este o sumă infinită, dar aceasta este suma unei progresii geometrice descrescătoare; există o formulă pentru aceasta: . Zona fulgului de nea este .

4. Dimensiunea fractală este egală cu log4/log3 = log 3 4 ≈ 1,261859... . Calculul precis va necesita un efort considerabil și explicații detaliate, așa că aici este mai degrabă o ilustrare a definiției dimensiunii fractale. Din formula legii puterii N(δ ) ~ (1/δ )D, Unde N- numărul de pătrate care se intersectează, δ - mărimea lor, și D este dimensiunea, o înțelegem D= jurnal 1/ δ N. Această egalitate este adevărată până la adăugarea unei constante (aceeași pentru toate δ ). Figurile arată a cincea iterație de construire a curbei Koch; pătratele grilei care se intersectează cu aceasta sunt umbrite în verde. Lungimea segmentului original este 1, deci în figura de sus lungimea laturii pătratelor este 1/9. 12 pătrate sunt umbrite, log 9 12 ≈ 1,130929... . Nu prea seamănă încă cu 1.261859... . Să privim mai departe. În imaginea din mijloc, pătratele au jumătate din dimensiune, dimensiunea lor este 1/18, umbrită 30. log 18 30 ≈ 1,176733... . Deja mai bine. Mai jos, pătratele sunt încă la jumătate mai mari; 72 de piese au fost deja pictate. log 72 30 ≈ 1,193426... . Chiar mai aproape. Apoi trebuie să creșteți numărul de iterații și, în același timp, să micșorați pătratele, apoi valoarea „empirică” a dimensiunii curbei Koch se va apropia constant de log 3 4, iar în limită va coincide complet.

Opțiuni

Fulgul de zăpadă Koch „dimpotrivă” se obține dacă construim curbe Koch în interiorul triunghiului echilateral original.

replici Cesaro. În loc de triunghiuri echilaterale, se folosesc triunghiuri isoscele cu un unghi de bază de la 60° la 90°. În figură, unghiul este de 88°.

Opțiune pătrată. Aici pătratele sunt completate.

Fulgul de nea Koch

pânză(
chenar: 1px negru punctat;
}

var cos = 0,5,
sin = Math.sqrt(3) / 2,
deg = Math.PI / 180;
canv, ctx;

funcția rebro(n, len) (
ctx.save(); // Salvați transformarea curentă
if (n == 0) ( // Caz non-recursiv - trage o linie
ctx.lineTo(len, 0);
}
altfel(
ctx.scale(1 / 3, 1 / 3); // Micșorează de 3 ori
rebro(n-1, len); //RECURSIUNE pe muchie
ctx.rotate(60 * grade);
rebro(n-1, len);
ctx.rotate(-120 * grade);
rebro(n-1, len);
ctx.rotate(60 * grade);
rebro(n-1, len);
}
ctx.restore(); // Restabiliți transformarea
ctx.translate(len, 0); // merge la capătul marginii
}

funcția drawKochSnowflake(x, y, len, n) (
x = x - len / 2;
y = y + len / 2 * Math.sqrt(3)/3;
ctx.save();
ctx.beginPath();
ctx.translate(x, y);
ctx.moveTo(0, 0);
rebro(n, len); ctx.rotate(-120 * grade); //RECUUURSION este deja un triunghi
rebro(n, len); ctx.rotate(-120 * grade);
rebro(n, len); ctx.closePath();
ctx.strokeStyle = "#000";
ctx.stroke();
ctx.restore();
}

funcția clearcanvas())( //șterge pânza
ctx.save();
ctx.beginPath();

// Folosiți matricea de identitate în timp ce ștergeți pânza
ctx.setTransform(1, 0, 0, 1, 0, 0);
ctx.clearRect(0, 0, canvas1.width, canvas1.height);

// Restabiliți transformarea
ctx.restore();
}

funcția run() (
canv = document.getElementById("canvas1");
ctx = canv.getContext("2d");
var numberiter = document.getElementById("qty").value;
drawKochSnowflake(canv.width/2, canv.height/2, 380, numberiter);

Ctx.stroke(); //redare
}

Fulgul de zăpadă al lui Koch - exemplu

Scrierea unei funcții care se numește recursiv este o modalitate de a genera o diagramă fractală pe ecran. Cu toate acestea, ce se întâmplă dacă ați dori ca rândurile din Cantor de mai sus să fie setate ca obiecte separate care ar putea fi mutate independent? Funcția recursivă este simplă și elegantă, dar nu vă permite să faceți mult dincolo de simpla creare a șablonului în sine.

Iată regulile. Curba Koch și alte modele fractale sunt adesea numite „monstri matematici”. Acest lucru se datorează paradoxului ciudat care apare atunci când aplicați definiția recursivă de nenumărate ori. Dacă lungimea liniei inițiale de pornire este una, prima iterație a curbei Koch va da o lungime a liniei de patru treimi. Fă-o din nou și obții șaisprezece și nouă. Pe măsură ce iterați în infinit, lungimea curbei Koch se apropie de infinit. Cu toate acestea, se încadrează în spațiul finit minuscul oferit chiar aici pe această lucrare!

Primele etape ale construirii curbei Koch

Deoarece lucrăm pe Pământul procesării pixelilor finiți, acest paradox teoretic nu va fi un factor pentru noi. Am putea proceda în același mod ca și cu setul Cantor și să scriem o funcție recursivă care aplică iterativ regulile lui Koch din nou și din nou. Cu toate acestea, vom rezolva această problemă în mod diferit, tratând fiecare segment al curbei Koch ca un obiect separat. Acest lucru va deschide câteva posibilități de proiectare. De exemplu, dacă fiecare segment este un obiect, putem permite fiecărui segment să se miște independent de locația sa inițială și să participe la simularea fizică.

Proprietățile de bază ale curbei Koch

1. Este continuu, dar nicaieri diferentiabil. În linii mari, tocmai acesta este motivul pentru care a fost inventat - ca exemplu al acestui tip de „ciudați” matematici.

2. Are lungime infinită. Fie lungimea segmentului inițial egală cu 1. La fiecare pas de construcție înlocuim fiecare dintre segmentele care alcătuiesc linia cu o linie întreruptă, care este de 4/3 ori mai lungă. Aceasta înseamnă că lungimea întregii linii întrerupte este înmulțită cu 4/3 la fiecare pas: lungimea liniei cu număr n este egal cu (4/3) n–1 . Prin urmare, linia limită nu are de ales decât să fie infinit de lungă.

În plus, am putea folosi culoare aleatoare, grosimea liniei etc. Pentru a afișa fiecare segment diferit. Pentru a ne îndeplini sarcina de a trata fiecare segment ca pe un obiect separat, trebuie mai întâi să decidem ce ar trebui să facă obiectul. Ce caracteristici ar trebui să aibă?

Să ne uităm la ce avem. Cu elementele de mai sus, cum și unde aplicăm regulile și principiile recursiunii lui Koch? În această simulare, am urmărit întotdeauna două generații: cea actuală și următoarea. Când am terminat de calculat generația următoare, acum a devenit relevant și am trecut la calculul noii generații următoare.

Vom folosi o tehnică similară aici. Așa arată codul. Desigur, cele de mai sus exclud „lucrarea” propriu-zisă aici care definește aceste reguli. Cum împărțim un segment de linie în patru, așa cum este descris de reguli? Construcția unui fractal se bazează pe conceptul de infinit. Pasul 2: Vom împărți acest segment în trei părți egale și vom ridica un triunghi echilateral pe partea centrală. Pasul 3: Pe cele patru noi segmente vom efectua pasul.

Intersectați instrumentul dintre cele două obiecte, faceți clic pe cerc. Fulgul de zăpadă Koch este o curbă fractală specială construită de matematicianul Koch, începând cu dantela lui Koch. Aceasta este o curbă trasată de-a lungul laturilor unui triunghi echilateral. Sireturile Koch sunt construite pe fiecare parte a triunghiului.

Fie latura triunghiului regulat original egal cu A. Apoi zona sa. Mai întâi latura este 1 și aria este: . Ce se întâmplă pe măsură ce iterația crește? Putem presupune că mici triunghiuri echilaterale sunt atașate unui poligon existent. Prima dată sunt doar 3, iar de fiecare dată sunt de 4 ori mai mulți decât precedentul. Adică pe n La pasul al treilea, se vor completa T n = 3 · 4 n–1 triunghiuri. Lungimea laturii fiecăreia dintre ele este o treime din latura triunghiului completat în pasul anterior. Aceasta înseamnă că este egal cu (1/3) n. Arii sunt proporționale cu pătratele laturilor, deci aria fiecărui triunghi este . Pentru valori mari n Apropo, acest lucru este foarte puțin. Contribuția totală a acestor triunghiuri la aria fulgului de zăpadă este T n · S n = 3/4 · (4/9) n · S 0 . Prin urmare după n pasul, aria figurii va fi egală cu suma S 0 + T 1 · S 1 + T 2 · S 2 + ... + T n · S n = . Un fulg de nea se obține după un număr infinit de pași, care corespunde lui n → ∞. Rezultatul este o sumă infinită, dar aceasta este suma unei progresii geometrice descrescătoare; există o formulă pentru aceasta: . Aria fulgului de nea este egală.

Următorul tabel prezintă primii pași în construirea unei curbe. Pentru a crea un fractal, trebuie pur și simplu să inserați trei copii ale curbei de-a lungul laturilor triunghiului. Rețineți că a doua figură este Steaua lui David. Rezultatul final este o curbă închisă construită pe un triunghi echilateral. Se poate observa că frita conține o stea cu șase colțuri. Designul este foarte asemănător cu unul pentagonal fractal.

Există o altă modalitate de a construi fulgi de zăpadă. Construcția descrisă mai sus poate fi definită ca o construcție prin adunare, deoarece figura de pornire, triunghiul, adaugă alte elemente. Există o substructură care îndepărtează elemente în loc de forma originală.

4. Dimensiunea fractală este egală cu log4/log3 = log 3 4 ≈ 1,261859... . Calculul precis va necesita un efort considerabil și explicații detaliate, așa că aici este mai degrabă o ilustrare a definiției dimensiunii fractale. Din formula legii puterii N(δ) ~ (1/δ)D, unde N- numărul de pătrate care se intersectează, δ - dimensiunea lor, D- dimensiune, obținem că D = log 1/δ N. Această egalitate este adevărată până la adăugarea unei constante (la fel pentru toate δ ). Figurile arată a cincea iterație de construire a curbei Koch; pătratele grilei care se intersectează cu aceasta sunt umbrite în verde. Lungimea segmentului original este 1, deci în figura din stânga lungimea laturii pătratelor este 1/9. 12 pătrate sunt umbrite, log 9 12 ≈ 1,130929... . Nu prea seamănă încă cu 1.261859... . Să privim mai departe. În imaginea din mijloc, pătratele au jumătate din dimensiune, dimensiunea lor este 1/18, umbrită 30. log 18 30 ≈ 1,176733... . Deja mai bine. În dreapta, pătratele sunt încă la jumătate mai mari, 72 de piese au fost deja pictate. log 72 30 ≈ 1,193426... . Chiar mai aproape. Apoi trebuie să creșteți numărul de iterații și, în același timp, să micșorați pătratele, apoi valoarea „empirică” a dimensiunii curbei Koch se va apropia constant de log 3 4, iar în limită va coincide complet.

Opțiuni

Fulgul de zăpadă Koch „dimpotrivă” se obține dacă construim curbe Koch în interiorul triunghiului echilateral original.

Linii Cesaro. În loc de triunghiuri echilaterale, se folosesc triunghiuri isoscele cu un unghi de bază de la 60° la 90°. În figură, unghiul este de 88°.

Varianta pătrată. Aici pătratele sunt completate.

Analogi tridimensionali. Spațiul Koch.

Fulgul de nea Koch

La începutul secolului al XX-lea, matematicienii căutau curbe care să nu aibă în niciun punct o tangentă. Aceasta însemna că curba și-a schimbat brusc direcția și cu o viteză enorm de mare (derivata era egală cu infinitul). Căutarea acestor curbe nu a fost cauzată doar de interesul inactiv al matematicienilor. Cert este că la începutul secolului al XX-lea mecanica cuantică s-a dezvoltat foarte rapid. Cercetătorul M. Brown a schițat traiectoria de mișcare a particulelor în suspensie în apă și a explicat acest fenomen după cum urmează: atomii în mișcare aleatoriu ai lichidului lovesc particulele suspendate și, prin urmare, le pun în mișcare. După această explicație a mișcării browniene, oamenii de știință s-au confruntat cu sarcina de a găsi o curbă care să aproximeze cel mai bine mișcarea particulelor browniene. Pentru a face acest lucru, curba trebuia să îndeplinească următoarele proprietăți: să nu aibă tangentă în niciun punct. Matematicianul Koch a propus o astfel de curbă. Nu vom intra în explicații ale regulilor de construcție, ci pur și simplu îi vom prezenta imaginea, din care totul va deveni clar (Fig. 1.1.1).

Figura 1.1.1. Fulgul de nea Koch.

O proprietate importantă pe care o are limita fulgilor de zăpadă Koch este lungimea sa infinită. Acest lucru poate părea surprinzător pentru că suntem obișnuiți să ne ocupăm de curbele din cursurile de calcul. De obicei curbele netede sau cel puțin pe bucăți au întotdeauna o lungime finită (care poate fi verificată prin integrare). Mandelbrot, în acest sens, a publicat o serie de lucrări fascinante care explorează problema măsurării lungimii coastei Marii Britanii. Ca model el

Orez. 1.1.2. Construcția fulgului de zăpadă Koch.

a folosit o curbă fractală, care amintește de marginea unui fulg de zăpadă, cu excepția faptului că a introdus un element de aleatoriu pentru a ține cont de aleatorietatea din natură. Drept urmare, s-a dovedit că curba care descrie linia de coastă are o lungime infinită.

șervețelul și covorul lui Sierpinski

Un alt exemplu de fractal simplu auto-similar --- șervețel Sierpinski(Fig. 1.2.1), inventat de matematicianul polonez Waclaw Sierpinski în 1915. Termenul în sine şerveţel aparține lui Mandelbrot. În metoda de construcție de mai jos, începem cu o anumită regiune și eliminăm secvențial subregiuni interne. Mai târziu vom lua în considerare alte metode, în special folosind sisteme L, precum și bazate pe funcții iterate.

Figura 1.2.1. șervețel Sierpinski

Fie mulțimea inițială S 0 un triunghi echilateral împreună cu regiunea pe care o înconjoară. Să împărțim S0 în patru regiuni triunghiulare mai mici, conectând punctele medii ale laturilor triunghiului original cu segmente. Să înlăturăm interiorul micii zone triunghiulare centrale. Să numim mulţimea rămasă S 1 (Fig. 1.2.2). Repetăm apoi procesul pentru fiecare dintre cele trei triunghiuri mici rămase pentru a obține următoarea aproximare S 2 . Continuând în acest fel, obținem o succesiune de mulțimi imbricate S n a căror intersecție este formată de șervețelul S.

Orez. 1.2.2. Construcția unui șervețel Sierpinski

Evident, aria totală a pieselor aruncate în timpul construcției este exact egală cu aria triunghiului original. La primul pas, am aruncat ¼ parte din zonă. În pasul următor, am aruncat trei triunghiuri, cu aria fiecăruia egală cu ½ 2 din aria celui original. Raționând în acest fel, suntem convinși că ponderea totală a suprafeței aruncate a fost:

1/4 + 3 * (1/4 2) + 3 2 * (1/4 3) + … + 3 n-1 * (1/4 n) + … .

Această sumă este egală. Prin urmare, putem pretinde că setul S rămas, adică șervețelul, are o zonă de măsura zero. Acest lucru face din S un set „perfect”, în sensul că își împarte complementul într-un număr infinit de regiuni triunghiulare, având în același timp grosime zero.

Covorul Sierpinski este considerat un alt model fractal. Este construit după cum urmează: luați un pătrat, împărțiți-l în nouă pătrate și decupați pătratul central. Apoi se face o procedură similară cu fiecare dintre cele opt pătrate rămase. Și așa mai departe la infinit. Drept urmare, în loc de un pătrat întreg, obținem un covor cu un model simetric deosebit. Acest model a fost propus pentru prima dată de matematicianul Sierpinski, în cinstea căruia și-a primit numele. Un exemplu de covor Sierpinski poate fi văzut în Fig. 1.2.3.

Fulgul de nea fractal, unul dintre cele mai faimoase și misterioase obiecte geometrice, a fost descris de Helga von Koch la începutul secolului nostru. Potrivit tradiției, în literatura noastră se numește fulgul de zăpadă al lui Koch. Aceasta este o figură geometrică foarte „tepoasă”, care poate fi văzută metaforic ca rezultatul „înmulțirii” repetate a Stelei lui David de la sine. Cele șase raze principale ale sale sunt acoperite cu un număr infinit de vârfuri „ace” mari și mici. Fiecare fragment microscopic al conturului unui fulg de nea este ca două mazăre într-o păstaie, iar fasciculul mare, la rândul său, conține un număr infinit de aceleași fragmente microscopice.

La un simpozion internațional despre metodologia modelării matematice la Varna, în 1994, am întâlnit lucrările autorilor bulgari care au descris experiența lor de utilizare a fulgilor de nea lui Koch și a altor obiecte similare în lecțiile de liceu pentru a ilustra problema divizibilității spațiului și aporii filosofice ale lui Zenon. În plus, din punct de vedere educațional, în opinia mea, însuși principiul construirii structurilor geometrice fractale regulate este foarte interesant - principiul înmulțirii recursive a elementului de bază. Nu degeaba natura „iubește” formele fractale. Acest lucru se explică tocmai prin faptul că sunt obținute prin reproducere simplă și modificarea dimensiunii unui anumit bloc de construcție elementar. După cum știți, natura nu debordează cu o varietate de motive și, acolo unde este posibil, se mulțumește cu cele mai simple soluții algoritmice. Privește cu atenție contururile frunzelor și, în multe cazuri, vei găsi o relație clară cu forma conturului unui fulg de zăpadă Koch.

Vizualizarea structurilor geometrice fractale este posibilă numai cu ajutorul unui computer. Este deja foarte dificil să construiești manual un fulg de zăpadă Koch deasupra ordinului al treilea, dar chiar vrei să te uiți la infinit! Prin urmare, de ce să nu încercați să dezvoltați un program de calculator adecvat. În RuNet puteți găsi recomandări pentru construirea unui fulg de zăpadă Koch din triunghiuri. Rezultatul acestui algoritm arată ca un amestec de linii care se intersectează. Este mai interesant să combinați această figură din „bucăți”. Conturul unui fulg de zăpadă Koch este format din segmente de lungime egală înclinate la 0°, 60° și 120° față de axa x orizontală. Dacă le notăm 1, 2 și respectiv 3, atunci un fulg de nea de orice ordin va fi format din triplete succesive - 1, 2, 3, 1, 2, 3, 1, 2, 3... etc. Fiecare dintre aceste trei tipuri de segmente pot fi atașate celui precedent la unul sau celălalt capăt. Luând în considerare această circumstanță, putem presupune că conturul unui fulg de zăpadă este format din segmente de șase tipuri. Să le notăm 0, 1, 2, 3, 4, 5. Astfel, avem posibilitatea de a codifica un contur de orice ordin folosind 6 cifre (vezi figura).

Un fulg de nea de ordin superior este obținut de la un predecesor de ordin inferior prin înlocuirea fiecărei margini cu patru, conectate ca palmele îndoite (_/\_). Tipul de muchie 0 este înlocuit cu patru muchii 0, 5, 1, 0 și așa mai departe conform tabelului:

0	0 1 5 0
1	1 2 0 1
2	2 3 1 2
3	3 4 2 3
4	4 5 3 4
5	5 0 4 5

Un triunghi echilateral simplu poate fi considerat ca un fulg de zăpadă Koch de ordin zero. În sistemul de codificare descris, acesta corespunde intrării 0, 4, 2. Orice altceva poate fi obținut prin înlocuirile descrise. Nu voi furniza aici codul de procedură și, prin urmare, vă voi lipsi de plăcerea de a vă dezvolta propriul program. Când îl scrieți, nu este deloc necesar să folosiți un apel recursiv explicit. Poate fi înlocuit cu un ciclu obișnuit. În procesul de lucru, veți avea un alt motiv să vă gândiți la recursivitate și la rolul acesteia în formarea formelor cvasi-fractale ale lumii din jurul nostru și la sfârșitul drumului (dacă, desigur, nu sunteți prea leneș). pentru a o parcurge până la capăt) veți putea admira modelul complex al contururilor unui fulg de nea fractal și, de asemenea, să priviți în sfârșit în fața infinitului.