1 mechanical vibrations. Mechanical vibrations (basic school). According to the variant of interaction with the environment
1. Oscillations. Periodic fluctuations. Harmonic vibrations.
2. Free vibrations. Continuous and damped oscillations.
3. Forced vibrations. Resonance.
4. Comparison of oscillatory processes. Energy of sustained harmonic vibrations.
5. Self-oscillations.
6. Oscillations of the human body and their registration.
7. Basic concepts and formulas.
8. Tasks.
1.1. Fluctuations. Periodic fluctuations.
Harmonic vibrations
Fluctuations are called processes that differ in varying degrees of repeatability.
Recurring processes continuously occur inside any living organism, for example: heart contractions, lung function; we shiver when we are cold; we hear and speak due to vibrations of the eardrums and vocal cords; when we walk, our legs oscillate. The atoms of which we are made vibrate. The world we live in is surprisingly prone to hesitation.
Depending on the physical nature of the repeating process, oscillations are distinguished: mechanical, electrical, etc. This lecture discusses mechanical vibrations.
Periodic fluctuations
Periodic called such fluctuations in which all the characteristics of the movement are repeated after a certain period of time.
For periodic oscillations, the following characteristics are used:
oscillation period T, equal to the time during which one complete oscillation occurs;
vibration frequencyν, equal to the number of oscillations performed in one second (ν = 1 / T);
vibration amplitude A, equal to the maximum displacement from the equilibrium position.
Harmonic vibrations
A special place among periodic oscillations is occupied by harmonic fluctuations. Their importance is due to the following reasons. Firstly, oscillations in nature and in technology often have a character very close to harmonic, and, secondly, periodic processes of a different form (with a different dependence on time) can be represented as the superposition of several harmonic oscillations.
Harmonic vibrations- these are fluctuations in which the observed value changes over time according to the sine or cosine law:
In mathematics, functions of this kind are called harmonic, therefore, oscillations described by such functions are also called harmonic.
The position of the body performing the oscillatory motion is characterized by displacement relative to the equilibrium position. In this case, the quantities included in formula (1.1) have the following meaning:
NS- bias bodies at time t;
A - amplitude fluctuations equal to the maximum displacement;
ω - circular frequency oscillations (the number of oscillations performed in 2 π seconds) associated with the vibration frequency by the ratio
φ = (ωt +φ 0) - phase fluctuations (at time t); φ 0 - initial phase oscillations (at t = 0).
Rice. 1.1. Time displacement plots for x (0) = A and x (0) = 0
1.2. Free vibrations. Continuous and damped oscillations
Free or own are called such oscillations that occur in the system, left to itself, after it has been brought out of equilibrium.
An example is the vibrations of a ball suspended from a thread. In order to cause vibrations, you need to either push the ball, or, taking it to the side, release it. When pushing, the ball is told kinetic energy, and in case of deviation - potential.
Free vibrations are performed due to the initial supply of energy.
Free undamped vibrations
Free vibrations can be continuous only in the absence of friction force. Otherwise, the initial supply of energy will be spent on overcoming it, and the range of fluctuations will decrease.
As an example, consider the vibrations of a body suspended on a weightless spring that occur after the body is deflected down and then released (Fig. 1.2).
Rice. 1.2. Body vibrations on a spring
From the side of the stretched spring, the body acts elastic force F proportional to the amount of displacement NS:
The constant factor k is called spring rate and depends on its size and material. The sign "-" indicates that the elastic force is always directed in the direction opposite to the direction of displacement, i.e. to the equilibrium position.
In the absence of friction, the elastic force (1.4) is the only force acting on the body. According to Newton's second law (ma = F):
After transferring all the terms to the left side and dividing by the body mass (m), we obtain the differential equation of free vibrations in the absence of friction:
The value ω 0 (1.6) turned out to be equal to the cyclic frequency. This frequency is called own.
Thus, free vibrations in the absence of friction are harmonic if, upon deviation from the equilibrium position, elastic force(1.4).
Own circular frequency is the main characteristic of free harmonic oscillations. This value depends only on the properties of the oscillatory system (in the case under consideration, on the body mass and spring stiffness). In what follows, the symbol ω 0 will always be used to denote natural circular frequency(i.e. the frequency with which the oscillations would occur in the absence of frictional force).
Amplitude of free vibrations is determined by the properties of the oscillatory system (m, k) and the energy imparted to it at the initial moment of time.
In the absence of friction, free oscillations close to harmonic ones also arise in other systems: mathematical and physical pendulums (the theory of these issues is not considered) (Fig. 1.3).
Mathematical pendulum- a small body (material point), suspended on a weightless thread (Fig. 1.3 a). If the thread is deflected from the equilibrium position by a small (up to 5 °) angle α and released, then the body will oscillate with a period determined by the formula
where L is the length of the thread, g is the acceleration of gravity.
Rice. 1.3. Mathematical pendulum (a), physical pendulum (b)
Physical pendulum- a rigid body that oscillates under the action of gravity around a fixed horizontal axis. Figure 1.3 b schematically shows a physical pendulum in the form of a body of arbitrary shape, deflected from the equilibrium position by an angle α. The oscillation period of a physical pendulum is described by the formula
where J is the moment of inertia of the body about the axis, m is the mass, h is the distance between the center of gravity (point C) and the axis of the suspension (point O).
The moment of inertia is a quantity that depends on the mass of the body, its size and position relative to the axis of rotation. The moment of inertia is calculated using special formulas.
Free damped oscillations
Friction forces acting in real systems significantly change the nature of motion: the energy of the oscillatory system is constantly decreasing, and the oscillations either fade out or do not arise at all.
The resistance force is directed in the direction opposite to the movement of the body, and at not very high speeds is proportional to the magnitude of the speed:
The graph of such fluctuations is shown in Fig. 1.4.
As a characteristic of the degree of attenuation, a dimensionless quantity called logarithmic damping decrementλ.
Rice. 1.4. Displacement versus time for damped oscillations
Logarithmic damping decrement is equal to the natural logarithm of the ratio of the amplitude of the previous oscillation to the amplitude of the subsequent oscillation.
where i is the ordinal number of the vibration.
It is easy to see that the logarithmic damping decrement is found by the formula
Strong attenuation. At
if the condition β ≥ ω 0 is satisfied, the system returns to the equilibrium position without vibrating. This movement is called aperiodic. Figure 1.5 shows two possible ways to return to the equilibrium position during aperiodic movement.
Rice. 1.5. Aperiodic movement
1.3. Forced vibrations, resonance
Free vibrations in the presence of friction forces are damped. Continuous oscillations can be created using periodic external influences.
Forced such oscillations are called, during which the oscillating system is exposed to an external periodic force (it is called a driving force).
Let the driving force change according to the harmonic law
The forced oscillation graph is shown in Fig. 1.6.
Rice. 1.6. Plot of displacement versus time for forced oscillations
It is seen that the amplitude of the forced oscillations reaches the steady-state value gradually. The steady-state forced vibrations are harmonic, and their frequency is equal to the frequency of the driving force:
The amplitude (A) of steady-state forced oscillations is found by the formula:
Resonance is the achievement of the maximum amplitude of forced vibrations at a certain value of the frequency of the driving force.
If condition (1.18) is not satisfied, then the resonance does not arise. In this case, with an increase in the frequency of the driving force, the amplitude of the forced oscillations decreases monotonically, tending to zero.
The graphical dependence of the amplitude A of forced vibrations on the circular frequency of the driving force at different values of the damping coefficient (β 1> β 2> β 3) is shown in Fig. 1.7. This set of graphs is called resonance curves.
In some cases, a strong increase in the vibration amplitude at resonance is dangerous for the strength of the system. There are cases when resonance has led to the destruction of structures.
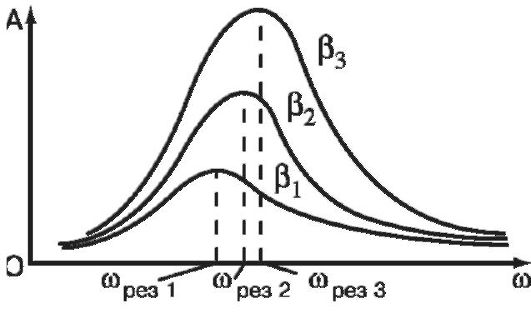Rice. 1.7. Resonance curves
1.4. Comparison of oscillatory processes. Energy of sustained harmonic vibrations
Table 1.1 shows the characteristics of the considered oscillatory processes.
Table 1.1. Characteristics of free and forced vibrations
Energy of sustained harmonic vibrations
A body performing harmonic vibrations has two types of energy: kinetic energy of motion E k = mv 2/2 and potential energy E p associated with the action of an elastic force. It is known that under the action of an elastic force (1.4), the potential energy of a body is determined by the formula E n = kx 2/2. For sustained vibrations NS= A cos (ωt), and the speed of the body is determined by the formula v= - А ωsin (ωt). From this, expressions are obtained for the energies of a body performing continuous oscillations:
The total energy of the system, in which undamped harmonic oscillations occur, is made up of these energies and remains unchanged:
Here m is the body mass, ω and A are the circular frequency and vibration amplitude, k is the coefficient of elasticity.
1.5. Self-oscillations
There are such systems that themselves regulate the periodic replenishment of lost energy and therefore can fluctuate for a long time.
Self-oscillations- undamped oscillations, supported by an external source of energy, the flow of which is regulated by the oscillating system itself.
Systems in which such oscillations occur are called self-oscillating. The amplitude and frequency of self-oscillations depend on the properties of the self-oscillating system itself. A self-oscillating system can be represented by the following diagram:
In this case, the oscillatory system itself acts as a feedback channel on the energy regulator, informing it about the state of the system.
Feedback the impact of the results of any process on its course is called.
If such an impact leads to an increase in the intensity of the process, then the feedback is called positive. If the impact leads to a decrease in the intensity of the process, then the feedback is called negative.
In a self-oscillating system, both positive and negative feedback can be present.
An example of a self-oscillating system is a clock in which the pendulum receives shocks due to the energy of a raised weight or a twisted spring, and these shocks occur at those moments when the pendulum passes through the middle position.
An example of biological self-oscillating systems are organs such as the heart and lungs.
1.6. Human body vibrations and their registration
The analysis of vibrations created by the human body or its individual parts is widely used in medical practice.
Oscillatory movements of the human body when walking
Walking is a complex periodic locomotor process resulting from the coordinated activity of the skeletal muscles of the trunk and limbs. Analysis of the walking process provides many diagnostic features.
A characteristic feature of walking is the frequency of the supporting position with one leg (period of single support) or two legs (period of double support). Normally, the ratio of these periods is 4: 1. When walking, there is a periodic displacement of the center of mass (CM) along the vertical axis (normally by 5 cm) and a deviation to the side (normally by 2.5 cm). In this case, the CM moves along a curve, which can be approximately represented by a harmonic function (Fig. 1.8).
Rice. 1.8. Vertical displacement of the CM of the human body during walking
Complex oscillatory movements while maintaining an upright position of the body.
A person standing upright has complex oscillations of the general center of mass (GCM) and the center of pressure (CP) of the feet on the plane of support. The analysis of these fluctuations is based on statokinesimetry- a method for assessing a person's ability to maintain an upright posture. By keeping the projection of the GCM within the coordinates of the boundary of the support area. This method is implemented using a stabilometric analyzer, the main part of which is a stabiloplatform, on which the subject is in a vertical position. Oscillations made by the subject's CP while maintaining an upright posture are transmitted to the stabiloplatform and recorded by special strain gauges. The load cell signals are transmitted to the recording device. In this case, it is written statokinesigram - trajectory of movement of the test subject's CP on a horizontal plane in a two-dimensional coordinate system. Harmonic spectrum statokinesigrams it is possible to judge about the features of verticalization in the norm and in case of deviations from it. This method allows you to analyze the indicators of statokinetic stability (SKU) of a person.
Mechanical vibrations of the heart
There are various methods for examining the heart, which are based on mechanical periodic processes.
Ballistocardiography(BCG) is a method for studying the mechanical manifestations of cardiac activity, based on the registration of pulse micromovements of the body, caused by the ejection of a push of blood from the ventricles of the heart into large vessels. In this case, the phenomenon arises recoil. The human body is placed on a special movable platform located on a massive stationary table. The platform, as a result of recoil, comes into a complex oscillatory motion. The dependence of the displacement of the platform with the body on time is called a ballistocardiogram (Fig. 1.9), the analysis of which makes it possible to judge the movement of blood and the state of cardiac activity.
Apexcardiography(AKG) is a method of graphical registration of low-frequency oscillations of the chest in the area of the apical impulse caused by the work of the heart. Registration of an apexcardiogram is performed, as a rule, on a multichannel electrocardiogram.
Rice. 1.9. Ballistocardiogram recording
ograph using a piezocrystalline sensor, which is a converter of mechanical vibrations into electrical ones. Before recording on the anterior chest wall, palpation determines the point of maximum pulsation (apical impulse), in which the sensor is fixed. An apexcardiogram is automatically built according to the sensor signals. An amplitude analysis of ACG is carried out - the amplitudes of the curve are compared at different phases of the heart with a maximum deviation from the zero line - the EO segment, taken as 100%. Figure 1.10 shows an apexcardiogram.
Rice. 1.10. Apexcardiogram recording
Kinetocardiography(CCG) is a method of recording low-frequency vibrations of the chest wall caused by cardiac activity. A kinetocardiogram differs from an apexcardiogram: the first records the absolute movements of the chest wall in space, the second records the vibrations of the intercostal space relative to the ribs. In this method, displacement (KKG x), speed of movement (KKG v) and acceleration (KKG a) for chest oscillations are determined. Figure 1.11 shows a comparison of different kinetocardiograms.
Rice. 1.11. Recording of kinetocardiograms of displacement (x), speed (v), acceleration (a)
Dynamocardiography(DCG) - a method for assessing the movement of the center of gravity of the chest. The dynamocardiograph allows you to register the forces acting from the side of the human chest. To record a dynamocardiogram, the patient is placed on a table lying on his back. Under the chest there is a sensing device, which consists of two rigid metal plates measuring 30x30 cm, between which there are elastic elements with strain gauges fixed on them. Periodically varying in size and place of application, the load acting on the sensing device is composed of three components: 1) constant component - the mass of the chest; 2) variable - the mechanical effect of respiratory movements; 3) variable - mechanical processes accompanying heart contraction.
The dynamocardiogram is recorded while holding the patient's breath in two directions: relative to the longitudinal and transverse axes of the receiving device. Comparison of various dynamocardiograms is shown in Fig. 1.12.
Seismocardiography based on the registration of mechanical vibrations of the human body caused by the work of the heart. In this method, with the help of sensors installed in the region of the base of the xiphoid process, a cardiac impulse is recorded due to the mechanical activity of the heart during the period of contraction. In this case, there are processes associated with the activity of tissue mechanoreceptors of the vascular bed, which are activated when the volume of circulating blood decreases. The seismic cardiac signal forms the form of oscillations of the sternum.
Rice. 1.12. Recording of normal longitudinal (a) and transverse (b) dynamocardiograms
Vibration
The widespread introduction of various machines and mechanisms into human life increases labor productivity. However, the work of many mechanisms is associated with the occurrence of vibrations that are transmitted to a person and have a harmful effect on him.
Vibration- forced vibrations of the body, in which either the whole body vibrates as a whole, or its separate parts vibrate with different amplitudes and frequencies.
A person constantly experiences various kinds of vibrational influences in transport, in production, in everyday life. Vibrations that have arisen in any part of the body (for example, the hand of a worker holding a jackhammer) propagate throughout the body in the form of elastic waves. These waves cause variable deformations of various types (compression, stretching, shear, bending) in the tissues of the body. The effect of vibrations on a person is due to many factors characterizing vibrations: frequency (frequency spectrum, fundamental frequency), amplitude, speed and acceleration of an oscillating point, energy of oscillatory processes.
Prolonged exposure to vibrations causes permanent disturbances in normal physiological functions in the body. Vibration sickness may occur. This disease leads to a number of serious disorders in the human body.
The influence that vibrations have on the body depends on the intensity, frequency, duration of vibrations, the place of their application and direction in relation to the body, posture, as well as on the state of the person and his individual characteristics.
Oscillations with a frequency of 3-5 Hz cause reactions of the vestibular apparatus, vascular disorders. At frequencies of 3-15 Hz, disorders associated with resonant vibrations of individual organs (liver, stomach, head) and the body as a whole are observed. Fluctuations with frequencies of 11-45 Hz cause visual impairment, nausea, and vomiting. At frequencies exceeding 45 Hz, damage to the vessels of the brain occurs, impaired blood circulation, etc. Figure 1.13 shows the areas of vibration frequencies that have a harmful effect on a person and systems of his organs.
Rice. 1.13. Frequency ranges of harmful effects of vibration on humans
At the same time, in a number of cases, vibrations are used in medicine. For example, using a special vibrator, the dentist prepares the amalgam. The use of high-frequency vibrating devices makes it possible to drill a hole with a complex shape in the tooth.
Vibration is also used in massage. During manual massage, the massaged tissues are set in vibrational motion with the help of the masseur's hands. During hardware massage, vibrators are used, in which tips of various shapes are used to transmit vibrational movements to the body. Vibration apparatuses are subdivided into apparatuses for general vibration, which cause shaking of the whole body (vibrating "chair", "bed", "platform", etc.), and apparatuses of local vibration impact on certain parts of the body.
Mechanotherapy
In physiotherapy exercises (exercise therapy), simulators are used, on which oscillatory movements of various parts of the human body are carried out. They are used in mechanotherapy - form of exercise therapy, one of the tasks of which is the implementation of dosed, rhythmically repetitive physical exercises in order to train or restore mobility in the joints on pendulum-type apparatus. The basis of these devices is a balancing one (from fr. balancer- swing, balance) a pendulum, which is a two-arm lever that performs oscillatory (swinging) movements about a fixed axis.
1.7. Basic concepts and formulas
Table continuation
Table continuation
End of the table
1.8. Tasks
1. Give examples of human vibrational systems.
2. In an adult, the heart beats 70 per minute. Determine: a) the frequency of contractions; b) the number of reductions in 50 years
Answer: a) 1.17 Hz; b) 1.84x10 9.
3. How long must a mathematical pendulum have for its oscillation period to be equal to 1 second?
4.
A thin, straight, homogeneous rod 1 m long is suspended by the end on an axis. Determine: a) what is the period of its oscillations (small)? b) what is the length of a mathematical pendulum with the same oscillation period?
5.
A body weighing 1 kg vibrates according to the law x = 0.42 cos (7.40t), where t is measured in seconds, and x is in meters. Find: a) the amplitude; b) frequency; c) full energy; d) kinetic and potential energies at x = 0.16 m.
6.
Estimate the speed at which a person walks with a stride length l= 0.65 m. Leg length L = 0.8 m; the center of gravity is at a distance H = 0.5 m from the foot. For the moment of inertia of the leg relative to the hip joint, use the formula I = 0.2mL 2.
7.
How can you determine the mass of a small body aboard a space station if you have a clock, a spring, and a set of weights at your disposal?
8.
The amplitude of the damped oscillations decreases in 10 oscillations by 1/10 of its original value. The oscillation period is T = 0.4 s. Determine the logarithmic decrement and damping factor.
Mechanical vibrations
1. Mechanical vibrations
1.1 Mechanical vibrations: harmonic, damped and forced vibrations
1.2 Self-oscillations
1.3 Decomposition of vibrations into a harmonic spectrum. Harmonic Analysis Application for Diagnostic Data Processing
1.4 Mechanical waves, their types and propagation speed
1.5 Energy characteristics of the wave
List of sources used
1. Mechanical vibrations
1.1 Mechanical vibrations: harmonic, damped and forced vibrations
Oscillations are processes that differ in varying degrees of repetition (swinging of a clock pendulum, vibrations of a string or tuning fork legs, voltage between capacitor plates in a radio receiver circuit, heart work).
Depending on the physical nature of the repeating process, oscillations are distinguished: mechanical, electromagnetic, electromechanical, etc. We will consider mechanical vibrations. Oscillations occurring in the absence of friction and external forces are called proper; their frequency depends only on the properties of the system.
The simplest are harmonic vibrations, i.e. such fluctuations in which the fluctuating quantity (for example, the deflection of a pendulum) changes with time according to the law of sine or cosine.
Differential Equation of Harmonic Oscillation
Consider the simplest oscillatory system: a ball of mass m is suspended by a spring.
In this case, the elastic force F1 balances the gravity force mg. If you move the ball to a distance NS, then a large elastic force will act on it (F 1 + F). The change in the elastic force according to Hooke's law is proportional to the change in the length of the spring or the displacement of the ball x:
where k is the stiffness of the spring. The "-" sign reflects the fact that displacement and force have opposite directions.
where (w 0 t + a 0) = a is the oscillation phase; a 0 - initial phase at t = 0; w 0 - circular vibration frequency; A is their amplitude.
So, the bias x changes over time according to the cosine law.
Consequently, the motion of a system under the action of a force of the form f = - kx is a harmonic oscillation.
For a spring pendulum we get:
The circular frequency is related to the usual n ratio:.
Energy at harmonic vibration
Let us find out how the kinetic Еk and potential Ep harmonic vibration energy. The kinetic energy is equal to:
, (4)where k = m w 0 2.
We find the potential energy from the potential energy formula for elastic deformation and using (3):
(5)Adding (4) and (5), taking into account the relation
, we get:E = E K + E P =
. (6)Thus, the total energy of a harmonic vibration remains constant in the absence of friction forces; during the oscillatory process, kinetic energy is converted into potential energy and vice versa.
Damped Oscillations
Oscillations occurring in a system in the absence of external forces (but in the presence of friction or radiation losses) are called free. The free vibration frequency depends on the properties of the system and the intensity of the losses.
The presence of friction leads to damped oscillations. Oscillations with decreasing amplitude are called damped.
Let us assume that, in addition to the quasi-elastic force, the forces of resistance of the medium (friction) act on the system, then Newton's second law has the form:
. (7)We confine ourselves to considering small oscillations, then the speed of the system will be small, and at low speeds the drag force is proportional to the value of the speed:
, (8)where r is the coefficient of resistance of the medium. Sign " - "due to the fact that F tr and V have opposite directions.
Substitute (8) into (7). Then
orWe denote
,
where b is the damping coefficient, w 0 is the angular frequency of natural vibrations. Then
The solution to this equation essentially depends on the sign of the difference: w 2 = w 0 2 -b 2, where w is the circular frequency of damped oscillations. Under the condition w 0 2 -b 2> 0, w is a real value and solution (3) will be as follows:
The graph of this function is shown in the figure.
Rice. 2. Damped oscillations.
The dotted line shows the change in amplitude: A = ± A 0 e - b t.
The period of damped oscillations depends on the coefficient of friction and is equal to:
(11)With an insignificant resistance of the medium (b2< From the formula expressing the law of decay of the amplitude of oscillations, one can make sure that the ratio of the amplitudes separated from each other by an interval of one period (T) remains constant throughout the damping process. Indeed, the amplitudes of the oscillations, separated by an interval of one period, are expressed as follows: This relationship is called
this relationship:
This value is called the logarithmic damping decrement for the period.
With a strong damping b 2> w02, it follows from formula (11) that the oscillation period is an imaginary value. In this case, the movement is of an aperiodic (non-periodic) nature - the system brought out of the equilibrium position returns to the equilibrium position without oscillating. Which of these ways the system comes to equilibrium depends on the initial conditions.
Forced vibrations. Resonance
Forced such oscillations are called that arise in an oscillatory system under the influence of an external periodically changing force (driving force). Let the driving force change with time according to the harmonic law: f = F0 cosW t, where F0 is the amplitude, W is the circular frequency of the driving force.
When drawing up the equation of motion, it is necessary to take into account, in addition to the driving force, also those forces that act in the system during free oscillations, that is, the quasi-elastic force and the force of resistance of the medium. Then the equation of motion (Newton's second law) will be written as follows:
Dividing this equation by m and transferring the terms with dx and d 2 x to the left, we obtain a non-homogeneous linear differential equation of the second order.
Oscillation characteristic
Phase determines the state of the system, namely the coordinate, speed, acceleration, energy, etc.
Cyclic frequency characterizes the rate of change in the phase of oscillations.
The initial state of the oscillatory system is characterized by initial phase
Oscillation amplitude A is the largest displacement from the equilibrium position
Period T- This is the period of time during which the point performs one full swing.
Oscillation frequency is the number of complete oscillations per unit of time t.
Frequency, cyclic frequency and oscillation period are related as
Types of vibrations
Oscillations that occur in closed systems are called free or own fluctuations. Oscillations that occur under the influence of external forces are called forced... Also meet self-oscillations(forced automatically).
If we consider oscillations according to changing characteristics (amplitude, frequency, period, etc.), then they can be divided into harmonic, fading, growing(and also sawtooth, rectangular, complex).
With free vibrations in real systems, energy losses always occur. Mechanical energy is consumed, for example, to perform work to overcome the forces of air resistance. Under the influence of the friction force, the amplitude of the oscillations decreases, and after a while the oscillations stop. Obviously, the more the forces of resistance to movement, the faster the oscillations stop.
Forced vibrations. Resonance
Forced vibrations are non-damping. Therefore, it is necessary to replenish energy losses for each period of oscillation. To do this, it is necessary to act on the oscillating body with a periodically changing force. Forced vibrations are performed with a frequency equal to the frequency of changes in the external force.
Forced vibrations
The amplitude of the forced mechanical vibrations reaches the highest value if the frequency of the driving force coincides with the frequency of the vibrational system. This phenomenon is called resonance.
For example, if you periodically pull the cord in time with its natural vibrations, then we will notice an increase in the amplitude of its vibrations.
If you move a wet finger along the edge of the glass, the glass will make a ringing sound. Although imperceptible, the finger moves intermittently and transfers energy to the glass in short portions, causing the glass to vibrate.
The walls of the glass also begin to vibrate if a sound wave is directed at it with a frequency equal to its own. If the amplitude becomes very large, the glass may even break. Due to the resonance during the singing of F.I. Chaliapin, crystal pendants of the chandeliers trembled (resonated). Resonance can also be seen in the bathroom. If you sing softly sounds of different frequencies, then resonance will occur at one of the frequencies.
In musical instruments, the role of resonators is played by parts of their bodies. A person also has his own resonator - this is the oral cavity, which amplifies the sounds emitted.
The resonance phenomenon must be taken into account in practice. In some phenomena it can be useful, in others it can be harmful. Resonance phenomena can cause irreversible damage to various mechanical systems, such as improperly designed bridges. So, in 1905, the Egyptian Bridge collapsed in St. Petersburg, when a horse squadron passed through it, and in 1940, the Tacoma Bridge in the United States collapsed.
The phenomenon of resonance is used when, with the help of a small force, it is necessary to obtain a large increase in the amplitude of the oscillations. For example, the heavy tongue of a large bell can be swayed with a relatively small force at a frequency equal to the natural frequency of the bell.
Themes of the USE codifier: harmonic oscillations; amplitude, period, frequency, phase of oscillations; free vibrations, forced vibrations, resonance.
Fluctuations - these are changes in the state of the system that are repeated in time. The concept of vibrations covers a very wide range of phenomena.
Fluctuations in mechanical systems, or mechanical vibrations- This is a mechanical movement of a body or a system of bodies, which has a repeatability in time and occurs in the vicinity of the equilibrium position. Equilibrium position is called a state of the system in which it can remain for an arbitrarily long time, without experiencing external influences.
For example, if the pendulum is deflected and released, then oscillations will begin. The equilibrium position is the position of the pendulum in the absence of deflection. In this position, the pendulum, if not touched, can remain indefinitely. When oscillating, the pendulum passes the equilibrium position many times.
Immediately after the deflected pendulum was released, it began to move, passed the equilibrium position, reached the opposite extreme position, stopped there for a moment, moved in the opposite direction, passed the equilibrium position again and returned back. One thing happened full swing... Further, this process will be periodically repeated.
Amplitude of body vibrations is the value of its greatest deviation from the equilibrium position.
Oscillation period - this is the time of one complete oscillation. We can say that during the period the body travels a path of four amplitudes.
Oscillation frequency is the reciprocal of the period:. Frequency is measured in hertz (Hz) and shows how many complete oscillations occur in one second.
Harmonic vibrations.
We will assume that the position of the oscillating body is determined by a single coordinate. The equilibrium position corresponds to the value. The main task of mechanics in this case is to find a function that gives the coordinate of the body at any time.
For a mathematical description of oscillations, it is natural to use periodic functions. There are many such functions, but two of them - sine and cosine - are the most important. They have many good properties and are closely related to a wide range of physical phenomena.
Since the sine and cosine functions are obtained from each other by shifting the argument by, you can limit yourself to only one of them. We will use cosine for definiteness.
Harmonic vibrations- these are oscillations at which the coordinate depends on time according to the harmonic law:
(1)
Let us find out the meaning of the quantities included in this formula.
A positive value is the largest value of the coordinate in absolute value (since the maximum value of the modulus of the cosine is equal to one), i.e., the greatest deviation from the equilibrium position. Therefore - the amplitude of the oscillations.
The cosine argument is called phase hesitation. The value equal to the phase value at is called the initial phase. The initial phase corresponds to the initial coordinate of the body:.
The quantity is called cyclic frequency... Let's find its connection with the oscillation period and frequency. One complete oscillation corresponds to a phase increment equal to radians:, whence
(2)
(3)
The cyclic frequency is measured in rad / s (radians per second).
In accordance with expressions (2) and (3), we obtain two more forms of writing the harmonic law (1):
The graph of function (1), expressing the dependence of the coordinate on time with harmonic oscillations, is shown in Fig. 1 .
The harmonic law of the form (1) is of the most general nature. He answers, for example, situations when two initial actions were performed simultaneously with the pendulum: they deflected it by an amount and gave it a certain initial velocity. There are two important special cases when one of these actions was not performed.
Let the pendulum be deflected, but the initial speed was not reported (released without the initial speed). It is clear that in this case, therefore, one can put. We get the cosine law:
The graph of harmonic oscillations in this case is shown in Fig. 2.
 |
| Rice. 2. Cosine law |
Let us now assume that the pendulum was not deflected, but the initial velocity was given to it by impact from the equilibrium position. In this case, so you can put. We get the sine law:
The oscillation graph is shown in Fig. 3.
 |
| Rice. 3. Sine law |
Equation of harmonic vibrations.
Let's return to the general harmonic law (1). We differentiate this equality:
. (4)
Now we differentiate the obtained equality (4):
. (5)
Let's compare expression (1) for the coordinate and expression (5) for the acceleration projection. We see that the projection of the acceleration differs from the coordinate only by a factor:
. (6)
This ratio is called harmonic vibration equation... It can be rewritten as follows:
. (7)
From a mathematical point of view, equation (7) is differential equation... Functions (not numbers, as in ordinary algebra) serve as solutions to differential equations.
So, you can prove that:
A solution to equation (7) is any function of the form (1) with arbitrary;
No other function is a solution to this equation.
In other words, relations (6), (7) describe harmonic oscillations with a cyclic frequency and only them. Two constants are determined from the initial conditions - according to the initial values of the coordinate and velocity.
Spring pendulum.
Spring pendulum is a spring-mounted weight capable of vibrating horizontally or vertically.
Let us find the period of small horizontal oscillations of the spring pendulum (Fig. 4). Oscillations will be small if the deformation of the spring is much less than its size. For small deformations, we can use Hooke's law. This will lead to the fact that the vibrations are harmonic.
We neglect friction. The load has a mass, the stiffness of the spring is equal.
The coordinate corresponds to the equilibrium position in which the spring is not deformed. Consequently, the amount of deformation of the spring is equal to the modulus of the coordinate of the load.
 |
| Rice. 4. Spring pendulum |
In the horizontal direction, only the spring force acts on the load. Newton's second law for cargo in projection onto the axis is:
. (8)
If (the load is shifted to the right, as in the figure), then the elastic force is directed in the opposite direction, and. On the contrary, if, then. The signs and are always opposite, so Hooke's law can be written as follows:
Then relation (8) takes the form:
We have obtained an equation of harmonic vibrations of the form (6), in which
The cyclic oscillation frequency of the spring pendulum is thus equal to:
. (9)
From here and from the ratio, we find the period of horizontal oscillations of the spring pendulum:
. (10)
If you suspend a weight on a spring, you get a spring-loaded pendulum that oscillates in the vertical direction. It can be shown that in this case, formula (10) is valid for the oscillation period.
Mathematical pendulum.
Mathematical pendulum is a small body suspended on a weightless inextensible thread (Fig. 5). A mathematical pendulum can oscillate in a vertical plane in a gravity field.
 |
| Rice. 5. Mathematical pendulum |
Let us find the period of small oscillations of the mathematical pendulum. The length of the thread is. We neglect the air resistance.
Let us write Newton's second law for the pendulum:
and project it onto the axis:
If the pendulum occupies a position as in the figure (i.e.), then:
If the pendulum is on the other side of the equilibrium position (i.e.), then:
So, for any position of the pendulum, we have:
. (11)
When the pendulum is at rest in the equilibrium position, equality is satisfied. For small oscillations, when the deviations of the pendulum from the equilibrium position are small (in comparison with the length of the thread), an approximate equality is fulfilled. We will use it in formula (11):
This is an equation of harmonic vibrations of the form (6), in which
Consequently, the cyclical frequency of oscillations of a mathematical pendulum is equal to:
. (12)
Hence the period of oscillation of the mathematical pendulum:
. (13)
Please note that formula (13) does not include the mass of the load. Unlike a spring pendulum, the period of oscillation of a mathematical pendulum does not depend on its mass.
Free and forced vibrations.
They say that the system does free vibrations if it is once taken out of the equilibrium position and then left to itself. No periodic external
At the same time, the system does not experience any influences, and there are no internal sources of energy that support the oscillations in the system.
The oscillations of the spring and mathematical pendulums considered above are examples of free oscillations.
The frequency with which free vibrations occur is called natural frequency oscillatory system. So, formulas (9) and (12) give the natural (cyclic) oscillation frequencies of the spring and mathematical pendulums.
In an idealized situation in the absence of friction, free oscillations are non-damping, i.e., they have a constant amplitude and last indefinitely. Friction is always present in real oscillatory systems, therefore free oscillations gradually damp (Fig. 6).
Forced vibrations- these are vibrations made by the system under the influence of an external force that periodically changes in time (the so-called driving force).
Let us assume that the natural frequency of the oscillations of the system is equal, and the driving force depends on time according to the harmonic law:
For some time, forced oscillations are established: the system makes a complex movement, which is an imposition of forced and free oscillations. Free oscillations gradually damp, and in the steady state the system performs forced oscillations, which also turn out to be harmonic. The frequency of steady-state forced oscillations coincides with the frequency
a forcing force (an external force imposes its frequency on the system, as it were).
The amplitude of the steady-state forced oscillations depends on the frequency of the driving force. The graph of this dependence is shown in Fig. 7.
 |
| Rice. 7. Resonance |
We see that resonance occurs near the frequency - the phenomenon of an increase in the amplitude of forced oscillations. The resonant frequency is approximately equal to the natural vibration frequency of the system:, and this equality is fulfilled the more accurately, the less friction in the system. In the absence of friction, the resonant frequency coincides with the natural vibration frequency, and the vibration amplitude increases to infinity at.
Fluctuations Are movements or processes that repeat exactly or approximately at certain intervals.
Mechanical vibrations fluctuations of mechanical values (displacement, speed, acceleration, pressure, etc.).
Mechanical vibrations (depending on the nature of the forces) are:
free;
forced;
self-oscillation.
Free called the vibrations that arise with a single action of an external force (initial energy transfer) and in the absence of external influences on the oscillatory system.
Free (or own)- these are oscillations in the system under the influence of internal forces, after the system is taken out of the state of equilibrium (in real conditions, free oscillations are always damped).
Free vibration conditions
1. The oscillatory system must have a stable equilibrium position.
2. When removing the system from the equilibrium position, a resultant force should arise that returns the system to its original position
3. The forces of friction (resistance) are very small.
Forced vibrations- vibrations occurring under the influence of external forces that change over time.
Self-oscillations- undamped oscillations in the system, supported by internal sources of energy in the absence of an external variable force.
The frequency and amplitude of self-oscillations is determined by the properties of the oscillatory system itself.
Self-oscillations differ from free oscillations by the independence of the amplitude from time and from the initial action that excites the oscillation process.
The self-oscillating system consists of: an oscillating system; energy source; feedback devices that regulate the flow of energy from an internal energy source into the oscillatory system.
The energy received from the source during the period is equal to the energy lost by the oscillatory system during the same time.
Mechanical vibrations are divided into:
fading;
undamped.
Damped Oscillations- vibrations, the energy of which decreases over time.
Oscillatory motion characteristics:
permanent:
amplitude (A)
period (T)
frequency ()
The greatest (in modulus) deviation of the oscillating body from the equilibrium position is called amplitude of oscillations. Usually, the amplitude is indicated by the letter A.
The period of time during which the body makes one complete vibration is called period of fluctuations.
The period of oscillation is usually denoted by the letter T and in SI it is measured in seconds (s).
The number of vibrations per unit of time is called vibration frequency.
The frequency is indicated by the letter v (“nu”). One vibration per second is taken as a unit of frequency. This unit is named hertz (Hz) in honor of the German scientist Heinrich Hertz.
the oscillation period T and the oscillation frequency v are related by the following relationship:
T = 1 / or = 1 / T.
Cyclic (circular) frequency ω- the number of oscillations in 2π seconds
Harmonic vibrations- mechanical vibrations that occur under the action of a force proportional to the displacement and directed opposite to it. Harmonic oscillations are performed according to the sine or cosine law.
Let the material point perform harmonic vibrations.
The harmonic vibration equation has the form:
a - acceleration V - speed q - charge A - amplitude t - time
