Miten hetken merkki määritetään? Statiikka. Voiman hetki. Luentojen peruskurssi materiaalien lujuudesta, teoriasta, käytännöstä, tehtävistä

Ohjeet

Olkoon Q piste, jonka suhteen voimamomenttia tarkastellaan. Tätä pistettä kutsutaan napaksi. Piirrä sädevektori r tästä pisteestä voiman F kohdistamispisteeseen. Tällöin voimamomentti M määritellään r:n vektorituloksi F:llä: M=.

Ristitulon tulos on vektori. Vektorin pituus ilmaistaan ​​moduulilla: |M|=|r|·|F|·sinφ, missä φ on r:n ja F:n välinen kulma. Vektori M on ortogonaalinen sekä vektoriin r että vektoriin F: M⊥r , M⊥F.

Vektori M on suunnattu siten, että vektorien r, F, M kolmoiskappale on oikea. Kuinka määrittää, että vektoreiden kolmoisosa on oikea? Kuvittele, että olet (silmäsi) kolmannen vektorin lopussa ja katsot kahta muuta vektoria. Jos lyhin siirtymä ensimmäisestä vektorista toiseen näyttää tapahtuvan vastapäivään, se on oikeakätinen vektorikolmois. Muuten olet tekemisissä vasenkätisen kolmion kanssa.

Yhdistä siis vektorien r ja F origot. Tämä voidaan tehdä siirtämällä vektori F rinnakkain pisteeseen Q. Piirrä nyt saman pisteen kautta akseli, joka on kohtisuorassa vektorien r ja F tasoon nähden. Tämä akseli on välittömästi kohtisuorassa vektoreihin nähden. Tässä on periaatteessa vain kaksi vaihtoehtoa voimamomentin ohjaamiseen: ylös tai alas.

Yritä suunnata voimamomentti F ylöspäin, piirrä vektorinuoli akselille. Katso tästä nuolesta vektoreita r ja F (voit käyttää symbolista silmää). Lyhin siirtymä r:stä F:ään voidaan osoittaa pyöristetyllä nuolella. Onko vektoreiden r, F, M kolmoinen oikein? Osoittaako nuoli vastapäivään? Jos kyllä, niin olet oikeassa suunnassa voimamomentille F. Jos ei, sinun on vaihdettava suunta päinvastaiseksi.

Voit myös määrittää voimamomentin suunnan oikean käden säännöllä. Kohdista etusormesi sädevektorin kanssa. Kohdista keskisormesi voimavektorin kanssa. Katso kahta vektoria peukalon päästä. Jos siirtyminen etusormesta keskisormeen suoritetaan vastapäivään, voimamomentin suunta on sama kuin peukalon osoittama suunta. Jos siirtymä tapahtuu myötäpäivään, niin voimamomentin suunta on sen vastainen.

Gimlet-sääntö on hyvin samanlainen kuin käsisääntö. Kierrä oikean kätesi neljällä sormella ruuvia kohdasta r asentoon F. Vektoritulolla on suunta, johon kiinnike kiertyy tällaisen mentaalisen kierron aikana.

Olkoon nyt piste Q samalla suoralla, joka sisältää voimavektorin F. Tällöin sädevektori ja voimavektori ovat kollineaariset. Tässä tapauksessa niiden vektoritulo degeneroituu nollavektoriksi ja sitä edustaa piste. Nollavektorilla ei ole tiettyä suuntaa, mutta sitä pidetään samansuuntaisena minkä tahansa muun vektorin kanssa.

Jotta kehoa pyörittävän voiman vaikutus voidaan laskea oikein, määritä sen käyttöpiste ja etäisyys tästä pisteestä pyörimisakseliin. Tämä on tärkeää erilaisten mekanismien teknisten ominaisuuksien määrittämiseksi. Moottorin vääntömomentti voidaan laskea, jos sen teho ja nopeus tunnetaan.

Tarvitset

• Viivain, dynamometri, takometri, testeri, Teslameter.

Ohjeet

Määritä piste tai akseli, jonka ympärillä keho on. Etsi piste, johon voima kohdistetaan. Yhdistä voiman kohdistamispiste ja pyörimispiste tai laske kohtisuoraa pyörimisakseliin nähden. Mittaa tämä etäisyys, se on "voiman käsi". Ota mittaukset metreinä. Mittaa voima newtoneina dynamometrillä. Mittaa käsivarren ja voimavektorin välinen kulma. Vääntömomentin laskemiseksi etsi voiman ja niiden välisen kulman sini M=F r sin(α). Tulos on newtoneina metriä kohti.

Teoreettinen mekaniikka. Statiikka:

Lähestyvien voimien järjestelmä
Määritelmä ja kolmen voiman lause
Suppenevien voimien resultantin graafinen määritelmä
Voiman analyyttinen tehtävä
Suppenevien voimien resultantin analyyttinen määritys
Konvergoivien voimien järjestelmän ehdot ja tasapainoyhtälöt
Ongelmanratkaisu
★ Tasapaino lähentyvän voimajärjestelmän vaikutuksesta

Voimapari teoria

Voimapari ja sen ominaisuudet
Pariekvivalenssilauseet
Voimaparien lisäys
Parijärjestelmien tasapaino

Tuodaan tasoinen voimajärjestelmä
Poinsot'n Lemma
Lause tasovoimajärjestelmän pelkistämisestä
Tasovoimajärjestelmän pienentämisen erikoistapaukset
Tasapainoinen voimajärjestelmä

Tasaisten sauvajärjestelmien tukireaktioiden määritys
★ Tasapaino yhdensuuntaisten voimien järjestelmän vaikutuksesta tasossa
Rinnakkaisvoimajärjestelmä
Mielivaltainen tasainen voimajärjestelmä
Mielivaltainen tasainen voimajärjestelmä. RGR 1
★ Tasaisen mielivaltaisen voimajärjestelmän tasapaino
Komposiittijärjestelmien laskenta
Komposiittijärjestelmien laskenta. RGR 2
★ Kappalejärjestelmän tasapaino 1
★ Kehojärjestelmän tasapaino 2
★ Kehojärjestelmän tasapaino 3
Tukireaktioiden graafinen määritys

aiheet:termeh:statics:moment_of_force_relative_to_center

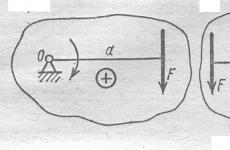
Tarkastellaan kappaletta, joka on kiinnitetty keskipisteeseen O ja joka voi pyöriä pisteen O kautta kulkevan akselin ympäri, joka on kohtisuorassa piirustustasoon nähden. Kohdistetaan voima P tämän kappaleen pisteeseen A ja selvitetään mikä määrää tämän voiman pyörimisliikkeen ( Kuva 1).

On selvää, että voiman vaikutus kehoon ei riipu vain sen suuruudesta, vaan myös siitä, miten se on suunnattu, ja se määräytyy lopulta sen mukaan. hetki keskustasta O.

Määritelmä 1. Voiman momentti P suhteessa keskipisteeseen O on voiman moduulin ja sen olakkeen tulo merkillä $\pm$ - eli momentin pisteestä suoralle lasketun kohtisuoran pituus voiman toiminnasta.

Merkisääntö: Voiman momentti katsotaan positiiviseksi, jos voima pyrkii pyörittämään kehoa vastapäivään ja negatiiviseksi, jos se kiertää kappaletta myötäpäivään.

Tämän määritelmän mukaan voimamomentti on numeerisesti yhtä suuri kuin kolmion OAB kaksoispinta-ala, joka on muodostettu voimavektorille P, jonka kärkipiste on momenttipisteessä: $M_0(P) = P\cdot d = 2S \Delta_(OAB)$ .

Ota huomioon, että voimamomentti suhteessa pisteeseen O on yhtä suuri kuin nolla, jos voiman vaikutuslinja kulkee momenttipisteen kautta.

Tarkoitettu voimamomentin määritelmä sopii vain tasovoimajärjestelmälle. Yleisessä tapauksessa, jotta voidaan yksiselitteisesti kuvata voiman pyörimisvaikutusta, otamme käyttöön seuraavan määritelmän.

Määritelmä 2. Voiman P vektori-momentti suhteessa keskustaan ​​O on vektori, joka:

sovelletaan momenttipisteessä O kohtisuorassa voimavektorille rakennetun kolmion tasoon nähden, jonka kärki on momenttipisteessä;

suunnattu oikean ruuvin säännön mukaan;

suuruudeltaan yhtä suuri kuin voimamomentti P suhteessa keskustaan ​​O (Kuva 1a).

Oikea ruuvisääntö, joka tunnetaan myös fysiikan kursseista nimellä gimlet-sääntö, tarkoittaa, että jos katsomme kohti vektorimomenttia $\vec(M_0)(\vec(P))$, näemme sen vaikutustason pyörimisen voimalla $\vec(P)$, joka tapahtuu vastapäivään .

Merkitään $\vec(r)$ voiman $\vec(P)$ kohdistamispisteen sädevektoria ja osoitetaan, että seuraava pitää paikkansa

Lause 1. Voiman $\vec(P)$ vektori-momentti suhteessa keskustaan NOIN on yhtä suuri kuin sädevektorin $\vec(r)$ ja voimavektorin $\vec(P)$ vektoritulo:

$$\vec(M_0)(\vec(P)) = (\vec(r) \times \vec(P))$$

Muista, että vektorien $\vec(a)\text( ja )\vec(b)$ vektoritulo on vektori $\vec(c)$ , joka ( Kuvio 2b):

on kohtisuorassa vektoreihin $\vec(a)\text( ja )\vec(b)$ ;

muodostaa niiden kanssa oikeanpuoleisen vektorin kolmion, eli se on suunnattu siten, että tätä vektoria kohti katsottuna näemme kierron vektorista $\vec(a)$ vektoriin $\vec( b)$ pienimmässä kulmassa vastapäivään;

suuruudeltaan kaksinkertainen näille vektoreille rakennetun kolmion pinta-alaan:

$$|\vec(c)| = |\vec(a) \times \vec(b)| = |\vec(a)|\cdot|\vec(b)|\cdot\sin(\vec(a),\,\vec(b))$$

Lauseen todistamiseksi huomaamme ensinnäkin, että vektori, joka on yhtä suuri kuin vektorien $\vec(r)\text( ja )\vec(P)$ vektoritulo, on kollineaarinen vektorin $\vec(M_0) kanssa. (\vec(P))$ .

Tämän varmistamiseksi riittää piirtää nämä vektorit yhdestä pisteestä ( Kuva 1c). Joten $(\vec(r) \times \vec(P)) \uparrow \uparrow \vec(M_0)(\vec(P))$.

Toiseksi näiden vektorien vektoritulon moduuli on yhtä suuri kuin:

$$|\vec(r) \times \vec(P)| = |\vec(r)|\cdot|\vec(P)|\cdot\sin(\vec(r),\,\vec(P)) = P \cdot d =|\vec(M_0)(\ vec(P))|$$

Tästä seuraa lauseen relaatio.

Tämän lauseen seuraus on:

Varignonin lause (konvergoituvien voimien resultantin momentista). Suppenevien voimien tuloksena olevan järjestelmän vektorimomentti suhteessa mielivaltaiseen keskustaan ​​O on yhtä suuri kuin järjestelmän kaikkien voimien vektorimomenttien geometrinen summa suhteessa tähän keskustaan:

$$\vec(M_0)(\vec(R)) = \sum_(i=1)^(i=n)\vec(M_(0\,\,i))(\vec(P_i))$$

Itse asiassa resultantin hetki, kun otetaan huomioon Lause 1 ja konvergoituvien voimien resultantin analyyttinen määritelmä on yhtä suuri:

$$ \vec(M_0)(\vec(R))= \vec(R)\times\vec(r) \,\,\,\;\;\text( , koska ) \vec(M_0 )(\ vec(P)) = (\vec(r) \times \vec(P)) \\ \vec(R)\times\vec(r)= \vec(r)\times\sum_(i= 1)^ (i=n)\vec(P_i) \,\,\,\;\;\text( , koska ) (\vec(P_1), \vec(P_2), \dots, \vec (P_n)) \sim \vec(R) = \sum_(i=1)^(i=n) \vec(P_i) \\ \vec(r)\times\sum_(i=1)^(i= n)\vec(P_i) ) = \sum_(i=1)^(i=n)(\vec(r)\times\vec(P_i)) = \sum_(i=1)^(i=n)\ vec(M_(0\) ,\,i))(\vec(P_i)) $$

Konvergoivien voimien tasojärjestelmässä geometrinen summa in Varignonin lause menee algebraan:

$$M_0(R)=\summa_(i=1)^(i=n)M_(0\,\,i)(\vec(P_i))$$

Huomautus

Oppikirjallisuudessa termillä "hetki" tarkoitetaan sekä voiman momenttia että sen vektori-momenttia.

Subjects/termeh/statics/moment_of_force_relative_to_center.txt · Viimeisimmät muutokset: 19.7.2013 19:53 - ¶

Voiman momentti suhteessa pisteeseen määräytyy voiman moduulin ja pisteestä voiman vaikutusviivaan lasketun kohtisuoran pituuden tulolla (kuva 4).

Kuva 4 – Voiman momentti F suhteessa pisteeseen O

Kun kappale on kiinnitetty pisteeseen O, voima F pyrkii pyörittämään sitä tämän pisteen ympäri. Pistettä O, josta momentti otetaan, kutsutaan hetken keskipisteeksi ja kohtisuoran a pituutta kutsutaan voiman käsivarreksi suhteessa hetken keskipisteeseen.

Voiman F momentti suhteessa O:iin määräytyy voiman ja varren tulon perusteella.

M O (F) = F·a.

Momenttia pidetään positiivisena, jos voima pyrkii pyörittämään kehoa myötäpäivään ja negatiivinen - vastapäivään. Kun voiman vaikutuslinja kulkee tietyn pisteen kautta, voiman momentti suhteessa tähän pisteeseen on nolla, koska tarkasteltavassa tapauksessa käsivarsi a = 0 (kuva 5).

Kuva 5 – Voiman momentin merkin määritys pisteen suhteen

Parin hetken ja voiman hetken välillä on yksi merkittävä ero. Voimaparin momentin numeerinen arvo ja suunta eivät riipu tämän parin sijainnista tasossa. Voimamomentin arvo ja suunta (merkki) riippuvat sen pisteen sijainnista, johon momentti määräytyy.

Tasovoimajärjestelmän tasapainoyhtälöt

Tasossa olevien voimien tasapainon ehdot: Tasossa mielivaltaisesti sijaitsevien voimien tasapainolle on välttämätöntä ja riittävää, että näiden voimien päävektori ja päämomentti suhteessa mihin tahansa keskustaan ​​ovat kumpikin erikseen nolla .

FGL = 0; M GL = Σ M O (F i) = 0.

Saamme tasapainoyhtälön perusmuodon:

Teoriassa momenttiyhtälöitä voidaan kirjoittaa ääretön määrä, mutta käytännössä kolme tasapainoyhtälöä riittää ratkaisemaan ongelmia tasossa. Kussakin erityistapauksessa käytetään yhtälöitä, joissa on yksi tuntematon.

Eri tapauksissa käytetään kolmea tasapainoyhtälöryhmää:

1. Tasapainoyhtälöiden ensimmäinen muoto

2. Tasapainoyhtälöiden toinen muoto

3. Tasapainoyhtälöiden kolmas muoto

Yhdensuuntaisten voimien järjestelmälle (kuva 43) voidaan laatia vain kaksi tasapainoyhtälöä:

Esimerkki.

Annettu: F = 24 kN; q = 6 kN/m; M = 12 kN m a = 60°; a = 1,8 m; b = 5,2 m; c = 3,0 m. Määritä reaktiot VA, H A ja V B (kuva 6).

Kuva 6 – Määritetty kaksitukipalkki

Hylkäämme liitokset (tuet A ja B), korvaamme niiden toiminnan reaktioilla: kiinteässä tuessa on reaktiot V A (pysty) ja H A (vaaka). Liikkuva tuki - reaktio V B (pysty). Valitsemme XY-koordinaattijärjestelmän, jonka origo on vasemmassa tuessa, määritämme jaetun kuorman resultantin:

Q = q·a2 = 6·5,2 = 31,2 kN.

Piirrämme palkin suunnittelukaavion (kuva 7).

Kuva 7 – Palkin suunnittelukaavio

Tuloksena olevalle mielivaltaiselle tasovoimajärjestelmälle laadimme tasapainoyhtälöt:

∑F ix = 0; H A – F cos60° = 0;

∑F i y = 0; V A – F cos30° – Q + V B = 0;

∑М А (Fi) = 0; Q·(1,8 + 2,6) + F·cos30°·(1,8 + 5,2) – M – V B · (1,8 + 5,2 + 3) = 0.

Ratkaisemme yhtälöjärjestelmän.

HA = F cos60° = 24 ± 0,5 = 12 kN;

V A = F cos30° + Q – V B = 24 0,866 + 31,2 – 27,08 = 24,9 kN.

Ratkaisun oikeellisuuden tarkistamiseksi laskemme momenttien summan suhteessa kaltevan voiman F vaikutuspisteeseen:

∑М А (F i) = V A · (1,8 + 5,2) – Q·2,6 – М – V B ·3 = 24,9·7 – 31,2·2,6 – 12 – 27, 08,3 = – 0,06.

Vastaus: palkin kannatusreaktiot ovat V A = 24,9 kN; VB = 27,08 kN; N A = 12 kN.

Kontrollikysymykset:

1. Mikä määrittää voimaparin vaikutuksen?

2. Riippuuko voimaparin vaikutus sen sijainnista tasossa?

3. Riippuvatko voimamomentin arvot ja suunta suhteessa pisteeseen tämän pisteen suhteellisesta sijainnista ja voiman vaikutuslinjasta?

4. Milloin pisteen ympärillä olevan voiman momentti on nolla?

5. Kuinka monta itsenäistä tasapainoyhtälöä voidaan muodostaa yhdensuuntaisten voimien tasojärjestelmälle?

Joka on yhtä suuri kuin olkapäänsä voiman tulo.

Voiman momentti lasketaan kaavalla:

Missä F-voimaa, l-voiman olkapää.

Voiman olkapää- tämä on lyhin etäisyys voiman vaikutuslinjasta kehon pyörimisakseliin. Alla oleva kuva esittää jäykkää runkoa, joka voi pyöriä akselin ympäri. Tämän kappaleen pyörimisakseli on kohtisuorassa kuvion tasoon nähden ja kulkee pisteen läpi, joka on merkitty kirjaimella O. Voiman olkapää Ft tässä on etäisyys l, pyörimisakselilta voiman toimintalinjaan. Se määritellään näin. Ensimmäinen vaihe on piirtää voiman toimintaviiva, sitten pisteestä O, jonka läpi kappaleen pyörimisakseli kulkee, lasketaan kohtisuora voiman vaikutuslinjaan nähden. Tämän kohtisuoran pituus osoittautuu tietyn voiman käsivarreksi.

Voiman momentti kuvaa voiman pyörivää toimintaa. Tämä toiminta riippuu sekä vahvuudesta että vipuvaikutuksesta. Mitä suurempi varsi, sitä vähemmän voimaa on käytettävä, jotta saavutetaan haluttu tulos, eli sama voimamomentti (katso kuva yllä). Siksi oven avaaminen on paljon vaikeampaa työntämällä sitä saranoiden lähelle kuin tarttumalla kahvaan, ja mutterin avaaminen pitkällä kuin lyhyellä jakoavaimella on paljon helpompaa.

Voimanmomentin SI-yksiköksi otetaan 1 N:n voimamomentti, jonka käsivarsi on 1 m - newtonmetri (N m).

Hetkien sääntö.

Jäykkä kappale, joka voi pyöriä kiinteän akselin ympäri, on tasapainossa, jos voimamomentti M 1 sen kääntäminen myötäpäivään on yhtä suuri kuin voimamomentti M 2 , joka kiertää sitä vastapäivään:

Momenttien sääntö on seurausta yhdestä mekaniikan lauseesta, jonka ranskalainen tiedemies P. Varignon muotoili vuonna 1687.

Pari voimaa.

Jos kappaleeseen vaikuttaa 2 samansuuruista ja vastakkain suunnattua voimaa, jotka eivät ole samalla suoralla, niin tällainen kappale ei ole tasapainossa, koska näiden voimien tuloksena oleva momentti suhteessa mihinkään akseliin ei ole nolla, koska molemmilla voimilla on samaan suuntaan suunnatut momentit. Kahta tällaista voimaa, jotka vaikuttavat samanaikaisesti kehoon, kutsutaan pari voimaa. Jos runko on kiinnitetty akselille, se pyörii voimaparin vaikutuksesta. Jos vapaaseen kappaleeseen kohdistetaan pari voimaa, se pyörii akselinsa ympäri. kulkee kehon painopisteen läpi, kuva b.

Voimaparin momentti on sama minkä tahansa akselin suhteen, joka on kohtisuorassa parin tasoon nähden. Totaalinen hetki M pari on aina yhtä suuri kuin yhden voiman tulo F etäisyyteen l voimien välillä, jota kutsutaan parin olkapää, riippumatta segmenteistä l, ja jakaa parin olkapään akselin sijainnin:

Useiden voimien momentti, joiden resultantti on nolla, on sama suhteessa kaikkiin toistensa suuntaisiin akseleihin, joten kaikkien näiden voimien vaikutus kehoon voidaan korvata yhden voimaparin vaikutuksella, jolla on samat voimat. hetki.

Luentojen peruskurssi materiaalien lujuudesta, teoriasta, käytännöstä, tehtävistä.

3.4. Merkkisääntö taivutusmomenteille ja leikkausvoimille.

Poikittaisvoimaa palkin osassa mn (kuva 3.7, a) pidetään positiivisena, jos ulkoisten voimien resultantti osan vasemmalla puolella on suunnattu alhaalta ylös ja oikealle - ylhäältä alas, ja negatiivinen - päinvastaisessa tapauksessa (kuva 3.7, b).

Taivutusmomentti palkin osassa, esimerkiksi poikkileikkauksessa mn (kuva 3.8, a), katsotaan positiiviseksi, jos ulkoisten voimien resultantti momentti osan vasemmalla puolella on suunnattu myötäpäivään ja oikealle - vastapäivään ja negatiivinen. päinvastaisessa tapauksessa (kuva 3.8 , b). Kuvassa näkyvät hetket. 3.8, a, taivuta palkkia kuperuudellaan alaspäin ja kuvassa 2 esitetyt momentit. 3.8, b, taivuta palkkia kuperuudellaan ylöspäin. Tämä voidaan helposti tarkistaa taivuttamalla ohutta viivainta.

Tämä tarkoittaa toista, helpompi muistaa, taivutusmomentin merkkisääntöä. Taivutusmomentti katsotaan positiiviseksi, jos kyseessä olevassa osassa palkki taipuu kuperasti alaspäin. Alla esitetään, että koverassa osassa sijaitsevat säteen kuidut kokevat puristusta ja kuperassa osassa jännitystä. Siten suostumalla piirtämään kaavion M positiiviset ordinaatit ylöspäin akselilta, saadaan, että diagrammi osoittautuu konstruoiduksi palkin puristettujen kuitujen puolelta.